Bart Vandereycken

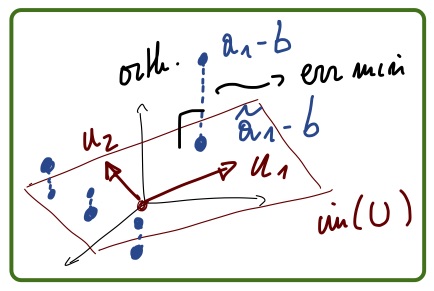
Low-rank approximations are a popular technique to reduce the dimension of large datasets in machine learning and solutions to high-dimensional problems in scientific computing. The course aims at covering the following topics: fundamentals (the best approximation problem, SVD, recap of linear algebra), large-scale computation of low-rank approximations (randomized methods), application in machine learning (principal component analysis, matrix completion), introduction to low-rank tensor formats (CP, matrix product states), computational methods for low-rank tensors (optimization, DMRG), application in scientific computing (ground states of spin systems, high-dimensional linear problems).

This course is a first year course in linear algebra.

The aim is to recognize and solve convex optimization problems. We cover a basic introduction to convex analysis, sets and functions. Theory also includes optimality conditions and duality, and theorems of alternative. We treat applications that lead to convex optimization problems in machine learning, statistics, signal processing, control, and finance. Specialised numerical algorithms include interior point methods and sub-gradient methods.

This course is an introduction to numerical analysis and scientific computing.

Approximation by low-rank tensors is a popular technique in the numerical simulation of certain high-dimensional problems (e.g. the electronic Schrödinger equation). Like a low-rank matrix, a low-rank tensor is a finite linear combination of certain lower dimensional tensors (multidimensional arrays). Contrary to matrices, however, they can scale to very high-dimensional problems or they have useful uniqueness properties for multi-way data analysis. This course will give an overview of applications and algorithms that use low-rank tensor techniques.

This course is an introduction to numerical continuous optimization: the mathematical formulation of optimization problems, the numerical algorithms to solve these problems together with their convergence and efficient implementation. An overview of existing software will be given and used during practical exercise sessions in MATLAB.

Covers largely the same mathematical topics as MAT201 (namely, limits, continuity, differentiation and integration for functions of several variables), but aimed at future physicists or students interested in applied math. Just like MAT201, this course introduces mathematical methods needed to understand real world questions involving quantities changing over time in 3-space but requires greater independence and maturity. Exams test for thorough conceptual understanding as well as computational fluency. In this course we assume that students will not need much help to master standard, straightforward calculations, allowing the instructor to emphasize more subtle aspects of the definitions and important exceptional cases that come up in applications. Offered Fall semester only.

Introduction to linear algebra, mostly in real n-space. Companion course to MAT201. Introduces more algebraic methods needed to understand real world questions. Whereas MAT201 develops calculus in a multivariable setting, this course develops fundamental algebraic tools involving matrices and vectors to study linear systems of equations and Gaussian elimination, linear transformations, orthogonal projection, least squares, determinants, eigenvalues and eigenvectors and their applications. Emphasizes concrete computations over more theoretical considerations. Because this is an algebra course, it is necessarily more abstract than MAT201, and requires some general arguments and consideration of exceptional cases on exams, mostly in the form of true/false questions, an intermediate between formal proofs and concrete computational questions.

Introduction to numerical methods with emphasis on algorithms, applications and computer implementation issues. Topics covered include solution of nonlinear equations; numerical differentiation, integration and interpolation; direct and iterative methods for solving linear systems; numerical solutions of differential equations; two-point boundary value problems; and approximation theory. This is an introductory course designed for upperclass undergraduates and beginning grad students in fields related to applied math and engineering. Special attention is paid to balancing implementation and algorithm development. Students are expected to accumulate hands-on experience by programming and running numerical simulations assigned as homework problems. Lectures are supplemented with numerical examples using MATLAB.