-
Cooperative phenomena and light-induced bistability in iron(II) spin-crossover compounds
A. Hauser, J. Jeftic, H. Romstedt, R. Hinek and H. Spiering
Coordination Chemistry Reviews, 190-192 (1999), p471-491


DOI:10.1016/S0010-8545(99)00111-3 | unige:2740 | Abstract | Article HTML | Article PDF
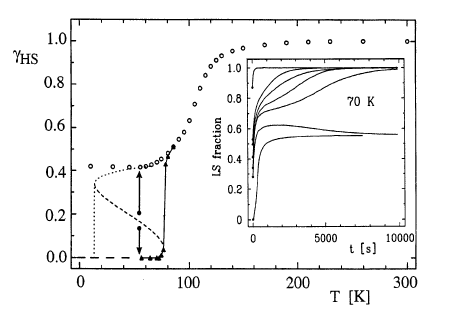
In iron(II) spin-crossover compounds, the transition from the 1A1 low-spin state at low temperatures to the 5T2 high-spin state at elevated temperatures is accompanied by a large increase in metal-ligand bond lengths. The resulting elastic interactions may be pictured as an internal pressure which is proportional to the concentration of the low-spin species. Because pressure stabilises the low-spin state relative to the high-spin state this results in a positive feedback. Thermal transition curves in neat iron(II) spin-crossover compounds are thus invariable much steeper than in diluted mixed crystals, and the high-spin→low-spin relaxation following the light-induced population of the high-spin state at low temperatures is self-accelerating. Strong interactions give rise to a thermal hysteresis, and light-induced bistabilities may be observed for compounds with initially a high-spin ground state and the potential for a light-induced population of the low-spin state. For such compounds, the increasing internal pressure may stabilise the low-spin state sufficiently so that it becomes the molecular ground state above some critical light-induced low-spin fraction. Secondary effects of the elastic interactions include crystallographic phase transitions, inhomogeneous distributions of sites, and anomalies such as steps in the transition curve.