EPDIC-7, Barcelona, May 2000

Powder Pattern Decomposition with the Aid of Preferred Orientation –

Use of whole Debye-Scherrer Ring

R. Cerny

Laboratoire de Cristallographie, Université de Genève, 24 Quai E. Ansermet, 1211 Genève 4, Switzerland

Keywords : Powder Pattern Decomposition, Preferred Orientation, Image Plate

Abstract. Method of the decomposition of overlapping reflections in a powder pattern with the aid of preferred orientation is tested on magnetically aligned samples using the effect of easy magnetization direction in hexagonal SmCo₅ and TbCo₅. Complete Debye-Scherrer rings, measured with an image plate detector, are integrated in different radial directions. The texture aided powder pattern decomposition results in correct values of structure amplitudes.

Introduction

Powder patterns collected at various values of a parameter which influences either the position or the intensity of a reflection can be used for the separation of overlapping profiles in the powder pattern. Preferred orientation (texture), which changes the intensity of reflections in a controlled manner, is an example of such parameter. The method is presented in [1], and an example of its application to a zeolite structure with 69 non-H atoms in the asymmetric unit is given in [2]. Another application using a simple empiric function for the preferred orientation correction is given in [3]. The texture aided pattern decomposition can be used with any type of the texture that is strong enough. It can be introduced by any suitable way. A uni-axial texture (distribution of a pole HKL has an axial symmetry in the sample coordinate system) introduced by a packing effect of grains with an anisotropic shape (plates or needles) was used in [3]. Different appearance of the texture in powder patterns was realized with a texture attachment allowing the c-inclination of the sample. The sample spinning has induced the axial symmetry of the pole distribution function. However, significant deviations of the texture from the uni-axial type were found. Especially the deviation from the so-called disc- or rod-shaped behavior of the crystallites (equal probability of all crystallite orientations around any pole HKL; see Condition II. in [4]; see also [5]) was considered as the main reason of the method failure. The texture of magnetically aligned powders is closer to an ideal uni-axial model, because only one direction – easy magnetization direction (EMD) – tends to orient preferentially (parallel to the magnetic field). When the texture axis is not parallel to the primary beam, the texture effect is visible as the intensity distribution on each Debye-Scherrer (DS) ring. Measurement of the whole DS ring and use of a two-dimensional detector accelerates considerably the data collection, as all information necessary for the pattern decomposition method is included in one image. The inclination angle c corresponds to the declination angle β measured from the vertical direction on the image. We have tested the method with magnetically aligned SmCo₅ and TbCo₅ and the image plate detector.

Theory

Correction for preferred orientation [4]

Let the distribution of poles HKL in a coordinate system of the sample be described by a function P_HKL(r = x,y,z) with one maximum in a general direction (Fig. 1). The distribution of poles hkl of any other plane, which makes only one angle f_H,hwith HKL, is given by

P_hkl (r₀) = (1 / 2p sin f_H,h) P_HKL (r) ds (1)

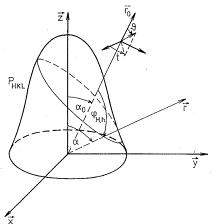where the integration is done along the closed curve, where are the poles HKL, which make the angle f_H,h with the pole hkl lying in the direction r₀. If the function P_HKL(r) is known, the function P_hkl(r₀) for any direction r₀ making an angle ₀ with the direction of the maximum of P_HKL(r) can be calculated. Regardless of the original shape of P_HKL(r), the function can be axially symmetrized by rapid sample spinning around one axis.

Figure 1. Schematic drawing of a pole

distribution function P_HKL.

The function P_HKL(r) can have the form :

P_HKL (a) = A exp (- G (1 - cosⁿ a)) (2)

where a is the angle between the spinning axis (preferred orientation axis) and r, G and n are free parameters, and A is the normalization constant. The case when the maximum (or minimum) of P_HKL (r) is inclined from the spinning axis, so-called inclined texture, can be treated by integration of Eq. 1 around the spinning axis [4].

Pattern decomposition using preferred orientation [3]

The factors in the formula for the intensity of a reflection hkl which depend on the orientation of the diffraction vector with respect to the sample coordinate system (in our case on a₀ - the angle between the diffraction vector and the preferred orientation axis) are: the absorption correction A and the preferred orientation correction P_hkl. The first term can be calculated, and parameters of unknown correction P_hkl can be determined from the ratio of intensities of non-overlapping reflections measured at different sample orientations (different angles a_0iin our case).

Once the correction for preferred orientation P_hkl is known for each reflection hkl and each sample orientation, the cluster of n overlapping reflections can be decomposed into individual intensities I_j(j = 1, n) if m cluster intensities I_{tot i} (m ≥ n) measured at m different sample orientations (different angles a_0i in our case) are available giving a system of m linear equations for n unknowns :

I_tot(a₀₁) = I₁(a₀₁) + I₂(a₀₁) + ... + I_n(a₀₁)

I_tot(a₀₂) = I₁(a₀₂) + I₂(a₀₂) + ... + I_n(a₀₂)

............................................................................. m ≥ n (3)

I_tot(a_0m) = I₁(a_0m) + I₂ (a_0m) + ... + I_n(a_0m)

Experimental

The method was tested on hexagonal (P6/mmm) SmCo₅ (a = 5.0271, c = 3.9899 Å) and TbCo₅ (a = 4.9765, c = 3.9952 Å). Both compounds are magnetically ordered. While SmCo₅ has EMD in the c-axis direction (axial), TbCo₅ has EMD perpendicular to the c-axis (basal), i.e. any vector in the basal plane. Fine powders of each compound were loosely enclosed in glass capillaries (0.5 mm diameter), which ensure that particles can re-orient under the magnetic field. A permanent magnet (Nd₂Fe₁₄B) oriented vertically, perpendicular to the capillary axis, was used to create the magnetic field of 0.3-0.5 T. All patterns were measured at the Swiss-Norwegian beam line (ESRF Grenoble) (l = 0.7995 Å, beam-size 0.6 x 0.6 mm) using MAR345 image plate (sample-IP distance 140 mm, exposition time 360 s). The images measured with the magnetic field show clearly the intensity distribution on DS rings due to the strong texture (Fig. 2).

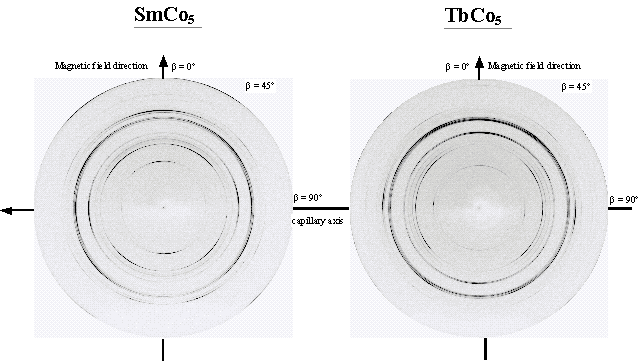
Figure 2. Images of diffraction patterns of magnetically aligned SmCo₅ and TbCo₅ (MAR345 image plate, Swiss-Norwegian beam line at the ESRF Grenoble, l = 0.7995 Å, beam-size 0.6 x 0.6 mm, sample-IP distance 140 mm, exposition time 360 s).

The images were integrated in seven different radial directions with different declination angles β (0, 15, 30, 45, 60, 75 and 90°) by using a program FIT2D (ESRF Grenoble). Resulting two-dimensional powder patterns were corrected for the absorption effect (μ = 1 mm^-1) using the formula given in the Fig. 3, which includes the dependence of the absorption correction on the off-equatorial position of the diffracted beam (generalization of the Eq. 2 in [6]). Corrected powder patterns (given in Fig. 4) were decomposed by Le Bail method using the program FULLPROF [7]. After that the decomposition of the overlapping reflections (closer then FWHM) was re-calculated by using the texture aided method described above. Pole 00l was chosen as the preferentially oriented pole HKL. The resolution in the orientation space was set to 4°, according to tests on simulated patterns [3]. The success of the pattern decomposition was estimated from the comparison of the observed squares of structure factors F²_obs (obtained from the pattern decomposition) and calculated ones F²_calc (obtained from the known structural model and put on the same scale as observed data). The results are given in Fig. 5.

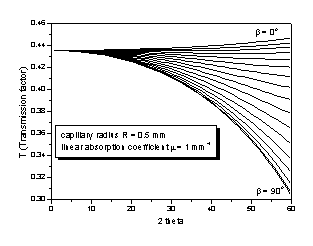T = 1/πR² ∫₀^R r ∫₀^2π exp[-μ(L + L’ sec α)] dυ dr

L = [R² – (r sin υ)²]^1/2 + r cos υ

L’ = [R² – (r sin (φ – υ))²]^1/2 - r cos (φ – υ)

tan φ = tan 2θ cos β

sin α = sin 2θ sin β

T – transmission factor

R – capillary radius

μ – linear absorption coefficient

θ – Bragg angle

β – declination angle

Figure 3. Transmission factor T for the case of a capillary with the diameter smaller than the primary beam. β is the declination angle measured on the DS ring (off-equatorial position of the diffracted beam). β = 0 corresponds to the vertical direction, capillary is horizontal.

Figure 4. Powder patterns as obtained by the integration of images in different radial directions and corrected for the absorption effect. β = 0º corresponds to the vertical direction (magnetic field direction).

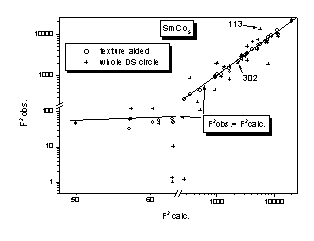
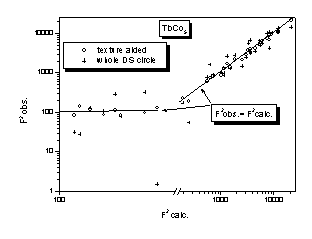
Figure 5. Observed (F²_obs) vs. calculated (F²_calc) values of squares of structure factors.

Discussion

One can see from the Fig. 5 a good success of the texture aided pattern decomposition. We have drawn for the comparison results of the decomposition when no texture information is used, and the integration of the images is performed on whole DS rings. The decomposition in that case yields the F²_obs, which are less reliable. The reasons are two: i) the texture is not completely eliminated by the integration around whole DS ring, ii) the decomposition suffers from the peak overlap. The success of texture aided pattern decomposition is demonstrated on two strongly overlapping SmCo₅ reflections 113 and 302 given in Fig. 6. As one can see from the Fig. 5 the F²_obs values of these two reflections as resulting from the decomposition are far from their correct values if no texture information is used.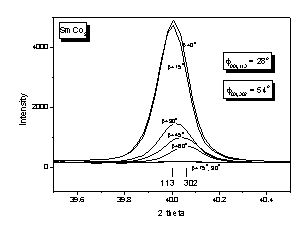

Figure 6. Two SmCo₅ overlapping reflections (113 and 302)

measured at different declination angles β. The angle

Φ between the preferentially oriented pole HKL

(00l in this case) and the pole hkl is given for

both reflections.

The preferred orientation of both samples can be correctly described by the uni-axial texture using a simple empiric function. Calculated 00l pole figures are given in Fig. 7. One can see that the model of the uni-axial texture with the maximum of the 00l pole distribution inclined by 90° with respect to the texture axis describes correctly the expected distribution of the 00l poles of TbCo₅ in the magnetic field. The correctness of the uni-axial texture model in both samples is further confirmed by the correct values of F²_obs obtained from the pattern decomposition using that texture model.

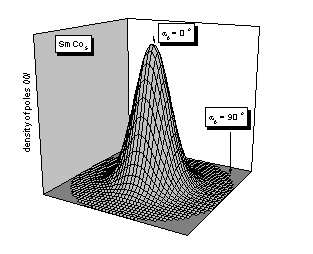
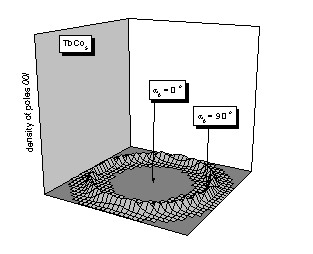
Figure 7. Calculated pole figures 00l for SmCo₅ resp. TbCo₅ corresponding to the axial resp. basal plane EMD. The parameters of the Eq. 2 are G = 19, n = 2 in both cases. The case of TbCo₅ was modeled as an inclined uni-axial texture with the inclination angle of 90°.

Two impurities were observed in the powder patterns of both samples: hexagonal and rhombohedral Sm₂Co₇ and Tb₂Co₇. We have tried the texture aided decomposition of peaks of the main phase (SmCo₅ or TbCo₅), which overlap with those of the impurities, using the texture of all three phases. The method, however, did not result in correct values, because the texture of impurity phases was not strong enough (G = 2). The contribution of impurity phases to the intensity of the measured patterns was therefore subtracted by using their known structural models.

Conclusions

Compounds showing EMD can be textured by a homogeneous magnetic field. The resulting texture is uni-axial and can be correctly described by a simple empiric preferred orientation function. Two compounds, hexagonal SmCo₅ and TbCo₅, were magnetically aligned. SmCo₅ shows the axial EMD and the resulting uni-axial distribution of the poles 00l has its maximum in the direction of the magnetic field. TbCo₅ shows basal EMD and the uni-axial distribution of the poles 00l has its maximum perpendicular to the rotation symmetry axis, which lies in the magnetic field direction. Complete Debye-Scherrer rings measured with an image plate detector allowed to characterize fully the preferred orientation and to decompose the overlapping reflections in the powder patterns. The decomposition resulted in correct values of the structure amplitudes. The texture aided powder pattern decomposition can be used also in the case of samples containing more unknown phases, if they show sufficiently strong texture.

Acknowledgements

The author want to thank to the staff of the Swiss-Norwegian Beamline (BM-1) at the ESRF Grenoble for the help with diffraction experiment. This work was supported by the Swiss National Science Foundation project no. 21-53847.98.

References

[1] M. Dahms & H.J. Bunge, Textures and Microstructures 6 (1986), 167 – 179.