TOAR
Description
TOAR is a memory efficient, and numerically reliable algorithm to compute the compact Arnoldi decomposition:
\[ \left[\begin{array}{cc} A & B \\ I & 0 \end{array} \right] \left[\begin{array}{c} Q_kR_{k,1}\\ Q_kR_{k,2} \end{array}\right] = \left[\begin{array}{c} Q_{k+1}R_{k+1,1}\\ Q_{k+1}R_{k+1,2} \end{array}\right] \underline H_{k+1}. \]
It is also a stabilized version of the SOAR procedure to compute the orthonormal basis \(Q_k\) of the second order Krylov subspace
\[ \mathcal{G}_k( A, B; r_{-1}, r_0)\equiv \mbox{span}\{ r_{-1}, r_0, r_1, \dots, r_{k-1}\} \quad\mbox{with}\quad r_ j= A r_{ j-1}+ B r_{ j-2}\quad \mbox{for}\quad j \ge 1. \]
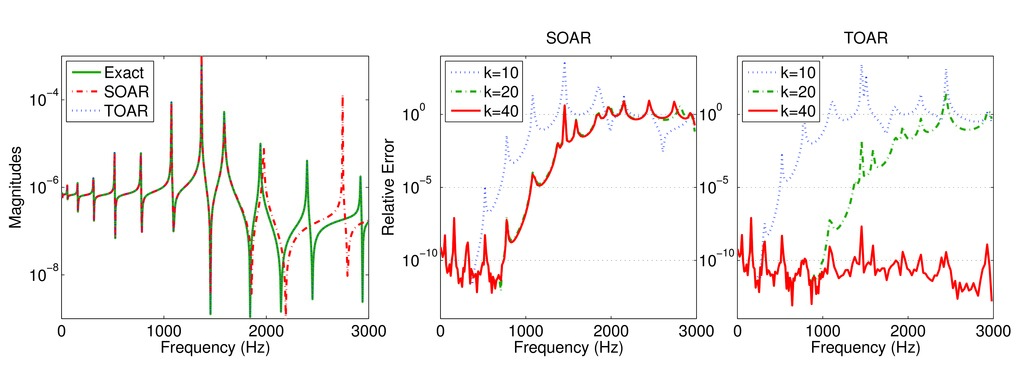
TOAR finds applications in nonlinear eigenvalue computation, and model order reduction. It demonstrates superior performance over the SOAR procedure.
Contents
MATLAB codes and data
Main files
Auxiliary files
Data and demo files for the numerical examples in Ref. [1].
Download link toar.tar.gz (updated on July 1st, 2015).
Examples
See Ref. [1] for details.
 |
References
Stability Analysis of the two-level orthogonal Arnoldi procedure
by Ding Lu, Yangfeng Su and Zhaojun Bai
SIAM J. Matrix Anal. Appl., 2016. 37(1): 195–214. (paper)SOAR: A second-order Arnoldi method for the solution of the quadratic eigenvalue problem
by Zhaojun Bai and Yangfeng Su
SIAM J. Matrix Anal. Appl., 2005. 26(3): 640-659.
Contact
Email: Ding.Lu@unige.ch
Homepage: http://www.unige.ch/~dlu