


Next: Bibliography
Numerical integration of differential equations with processors
Sergio Blanes, Fernando Casas, Ander Murua
Departament de Matemàtiques, Universitat Jaume I,
12071-Castellón, Spain.
sblanes@mat.uji.es
http://www3.uji.es/~sblanes
Contributed talk
Let us denote by
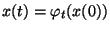 the solution of a differential
equation. A method,
the solution of a differential
equation. A method, 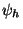 is of order
is of order 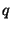 if
if
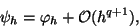 |
(1) |
and it is of effective order 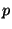 if there exist a map
if there exist a map 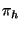 such that
[4]
such that
[4]
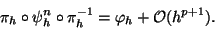 |
(2) |
Usually, 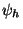 is referred as the kernel and
is referred as the kernel and 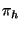 as the processor or corrector. Here,
as the processor or corrector. Here, 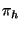 can be
used to solve many of the order conditions as well as to cancel
higher order non-correctable error terms [2,1].
This technique allow us to
obtain accurate results at the cost of
can be
used to solve many of the order conditions as well as to cancel
higher order non-correctable error terms [2,1].
This technique allow us to
obtain accurate results at the cost of 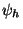 if the output is not
required frequently. We show that, if the non-correctable error terms
are small [5], the method will be very efficient, even if the
output is required frequently.
if the output is not
required frequently. We show that, if the non-correctable error terms
are small [5], the method will be very efficient, even if the
output is required frequently.
The same accuracy as with (2), applied for 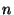 steps, can
essentially be obtained with
steps, can
essentially be obtained with
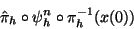 |
(3) |
where 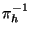 is usually expensive since it has to satisfy many
conditions, but it is computed only once, and
is usually expensive since it has to satisfy many
conditions, but it is computed only once, and 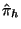 is a cheap
approximation to
is a cheap
approximation to 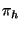 , obtained from the internal stages in the
computation of
, obtained from the internal stages in the
computation of 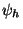 so, it is virtually cost-free [3].
so, it is virtually cost-free [3].



Next: Bibliography
Ernst Hairer
2002-05-22
![]() the solution of a differential
equation. A method,
the solution of a differential
equation. A method, ![]() is of order
is of order ![]() if
if
![]() steps, can
essentially be obtained with
steps, can
essentially be obtained with