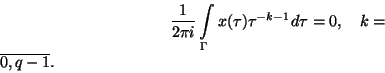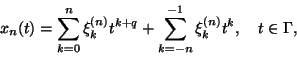Next: About this document ...
The numerical solution of singular integro-differential
equations in Hölder spaces
Caraus Iurie
Department of Mathematics and Informatics,
Moldova State University
Mateevici 60, str., Chisinau, Moldova,
MD-2009
caraush@usm.md
Contributed talk
Let 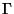 be a smooth Jordan border limiting the one-spanned area
be a smooth Jordan border limiting the one-spanned area  containing a point
containing a point 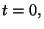
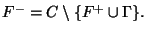 Let
Let 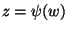 be a function, mapping conformably and unambiguously the
border
be a function, mapping conformably and unambiguously the
border 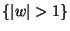 on the surface
on the surface 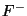 , so that
, so that
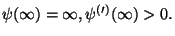 We denote
We denote
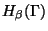 the spaces of
functions satisfying on
the spaces of
functions satisfying on 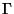 the Hölder condition with some
parameter
the Hölder condition with some
parameter 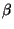
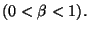 In the complex space
In the complex space
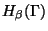 of functions
of functions 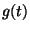 with norm
with norm
we will consider the singular integro-differential equations (SIDE)
![\begin{displaymath}
(Mx\equiv )\sum\limits_{r=0}^{q}\Big[ \tilde{A_r}(t)x^{(r)}...
...au )\cdot x^{(r)}(\tau
)d\tau \Big]=f(t),\quad t\in \Gamma ,
\end{displaymath}](img14.gif) |
(1) |
where
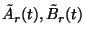 and
and
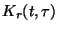
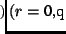 and
and 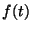 are given functions which belong to
are given functions which belong to
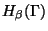 ;
;
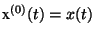 is the required functions;
is the required functions;
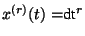
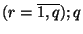 is a natural number which belong to
is a natural number which belong to
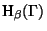 . We search the solution of equation (1) in the class of
functions, satisfying the condition
. We search the solution of equation (1) in the class of
functions, satisfying the condition
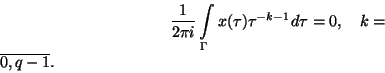 |
(2) |
We introduce the denomination ''the problem (1)-(2)'' for the SIDE (1)
together with the conditions (2). We search the approximate solution of the
problem (1)-(2) in the form
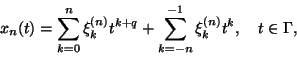 |
(3) |
where
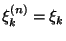
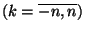 are unknowns numbers;
we will note that the function
are unknowns numbers;
we will note that the function 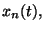 constructed by formula (3),
obviously, satisfies the condition (2).
We have elaborated the numerical schemes of the collocations method and
quadrature method for approximate solution of the SIDE. We investigate the
case when the equations defined on the arbitrary smooth boundaries. The
theoretical foundation of these methods have been obtained when the knots of
discretization forme a system of Feyer knots, and their convergence
is given in Hölder spaces.
constructed by formula (3),
obviously, satisfies the condition (2).
We have elaborated the numerical schemes of the collocations method and
quadrature method for approximate solution of the SIDE. We investigate the
case when the equations defined on the arbitrary smooth boundaries. The
theoretical foundation of these methods have been obtained when the knots of
discretization forme a system of Feyer knots, and their convergence
is given in Hölder spaces.



Next: About this document ...
Ernst Hairer
2002-05-23
![]() be a smooth Jordan border limiting the one-spanned area
be a smooth Jordan border limiting the one-spanned area ![]() containing a point
containing a point ![]()
![]() Let
Let ![]() be a function, mapping conformably and unambiguously the
border
be a function, mapping conformably and unambiguously the
border ![]() on the surface
on the surface ![]() , so that
, so that
![]() We denote
We denote
![]() the spaces of
functions satisfying on
the spaces of
functions satisfying on ![]() the Hölder condition with some
parameter
the Hölder condition with some
parameter ![]()
![]() In the complex space
In the complex space
![]() of functions
of functions ![]() with norm
with norm
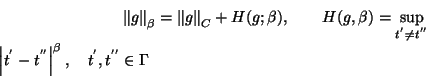
![\begin{displaymath}
(Mx\equiv )\sum\limits_{r=0}^{q}\Big[ \tilde{A_r}(t)x^{(r)}...
...au )\cdot x^{(r)}(\tau
)d\tau \Big]=f(t),\quad t\in \Gamma ,
\end{displaymath}](img14.gif)