


Next: Bibliography
One-step one-stage methods of order 2 and 3 for stiff ODEs
S.S. Filippov, M.V. Bulatov
Keldysh Institute of Applied Mathematics, 4 Miusskaya sq.,
125047 Moscow, Russia
Institute for System Dynamics and Control Theory,
134 Lermontova str., 664033 Irkutsk, Russia
Filippov@Keldysh.ru, mvbul@icc.ru
Contributed talk
For the problem
![\begin{displaymath}
x'(t)=f(x(t),t),\quad x(0)=x_0,\quad t\in[0,1]
\end{displaymath}](img1.gif) |
(1) |
with a sufficiently smooth function 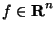 let us write down the explicit and the linearized implicit
Euler schemes:
let us write down the explicit and the linearized implicit
Euler schemes:
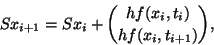 |
(2) |
where
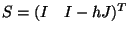 is a
is a
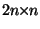 -matrix and
-matrix and
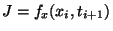 . Genrally, (2) has
no classical solution. By multiplying (2) by
. Genrally, (2) has
no classical solution. By multiplying (2) by 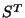 we arrive at
we arrive at
![\begin{displaymath}
S^TSx_{i+1}=x_i+hf(x_i,t_i)+(I-hJ)\{x_i+h[f(x_i,t_{i+1})-Jx_i]\}.
\end{displaymath}](img8.gif) |
(3) |
This is
a one-step one-stage method of order 2,  -stable,
with the stability function
-stable,
with the stability function
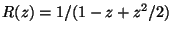 . When using
method (3) to solve numerically problem (1),
we have to solve a linear system
of
. When using
method (3) to solve numerically problem (1),
we have to solve a linear system
of 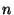 algebraic equations only [1].
algebraic equations only [1].
For a linear problem
![\begin{displaymath}
x'(t)=B(t)x(t)+g(t),\quad x(0)=x_0,\quad t\in[0,1]
\end{displaymath}](img12.gif) |
(4) |
with
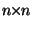 -matrix
-matrix 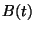 and
and
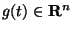 sufficiently smooth, one can construct
a one-step one-stage method of order 3.
Combining two one-step methods applied to (4) leads to the system
sufficiently smooth, one can construct
a one-step one-stage method of order 3.
Combining two one-step methods applied to (4) leads to the system
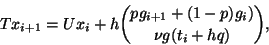 |
(5) |
of 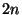 equations for
equations for 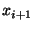 , where
, where
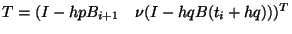 and
and
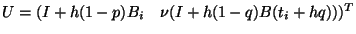 are
are
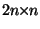 -matrices.
Genrally, (5) has no classical solution.
Multiplying (5) by
-matrices.
Genrally, (5) has no classical solution.
Multiplying (5) by 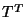 and choosing
and choosing
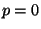 ,
, 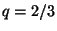 , and
, and 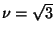 gives the desired method:
gives the desired method:
![\begin{displaymath}
\begin{array}{l}
\{I+3[I-2hB(t_i+2h/3)/3]^2\}x_{i+1}=
\{I+h...
...3]\}x_i+
h\{f_i+3[I-2hB(t_i+2h/3)/3]f(t_i+2h/3)\}.
\end{array}\end{displaymath}](img25.gif) |
(6) |
Again, we have to solve only a linear
algebraic system of 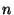 equations.
The method (6) is
equations.
The method (6) is 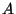 -stable with
-stable with
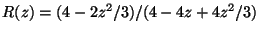 .
.
Numerical experiments with the methods (3) and (6)
were carried out for test problems taken from [2, (7.5.4)]
and [3, p. 13], respectively.



Next: Bibliography
Ernst Hairer
2002-05-24