


Next: Bibliography
Conservativity of symplectic schemes for the nonlinear
Schrödinger equation
Yifa Tang, Hua Guan, Quandong Feng
LSEC, ICMSEC, Academy of Mathematics and System Sciences,
Chinese Academy of Sciences, P.O. Box 2719,
Beijing 100080, P.R. China
tyf@lsec.cc.ac.cn
Contributed talk
We consider the nonlinear cubic Schrödinger equation (NLSE) with
initial conditions:
where
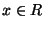 ,
, 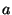 is a constant and
is a constant and 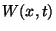 is a
complex function. Different initial conditions
is a
complex function. Different initial conditions 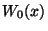 decide
different motions. For example, some kind of
decide
different motions. For example, some kind of 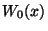 with
with
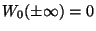 will produce bright solitons motion. It's
known that NLSE (1) has infinite conserved quantities such as the
energy, charge, momentum.
For equation (1), two popular spatial discretizations are
will produce bright solitons motion. It's
known that NLSE (1) has infinite conserved quantities such as the
energy, charge, momentum.
For equation (1), two popular spatial discretizations are
and
where 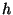 is the spatial step size and
is the spatial step size and
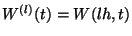 ,
,
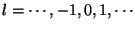 . These two discrete models are
nonstandard and standard hamiltonian systems respectively. (2a) is
the well-known Ablowitz-Ladik model. Analogously, (2a) has also
infinite conserved quantities, while (2b) has only two invariants:
the discrete energy and discrete charge.
For both models, we use some symplectic schemes to simulate the
solitons motions, and test the evolution of six discrete
invariants or approximations. And for (2a), two kind of
standardizing transformations suggested by Hairer, Lubich and
Wanner, and by Tang, Pérez-García and Vázquez are used.
The nice performance and conservativity of the symplectic schemes
is shown.
. These two discrete models are
nonstandard and standard hamiltonian systems respectively. (2a) is
the well-known Ablowitz-Ladik model. Analogously, (2a) has also
infinite conserved quantities, while (2b) has only two invariants:
the discrete energy and discrete charge.
For both models, we use some symplectic schemes to simulate the
solitons motions, and test the evolution of six discrete
invariants or approximations. And for (2a), two kind of
standardizing transformations suggested by Hairer, Lubich and
Wanner, and by Tang, Pérez-García and Vázquez are used.
The nice performance and conservativity of the symplectic schemes
is shown.



Next: Bibliography
Ernst Hairer
2002-04-17