Next: Bibliography
Adaptive integration of delay differential equation
M. Zennaro, A. Bellen
Dipartimento di Scienze Matematiche,
Università di Trieste,
I-34100 Trieste, Italy
zennaro@univ.trieste.it
Contributed talk
We consider the numerical solution of nonstiff delay differential equations (DDEs) of the
form
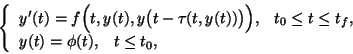
by means of variable stepsize continuous Runge-Kutta methods of discrete
(nodal) order 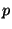 and uniform order
and uniform order 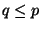 . Our aim is
to ensure, as far as possible, the proportionality of the maximum global error to
a given tolerance
. Our aim is
to ensure, as far as possible, the proportionality of the maximum global error to
a given tolerance 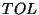 and to minimize the computational cost.
In this context,
and to minimize the computational cost.
In this context, 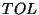 is meant as a tolerance per unit step.
The approach is explained in our forthcoming book [1, Chapter 7].
It is wellknown that, for ordinary differential equations (ODEs), the stepsize
control mechanism for a (discrete) advancing method of order
is meant as a tolerance per unit step.
The approach is explained in our forthcoming book [1, Chapter 7].
It is wellknown that, for ordinary differential equations (ODEs), the stepsize
control mechanism for a (discrete) advancing method of order 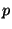 is mostly based on the use of
a second method, the error-estimating method, of different order
is mostly based on the use of
a second method, the error-estimating method, of different order 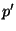 , usually
, usually 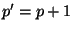 or
or 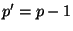 . The extension to DDE solvers is not straighforward, and its mathematical
justification is far from being obvious. However, the conclusions we arrive at are
consistent with the results already available in the literature.
In particular, we shall stress the following two points:
. The extension to DDE solvers is not straighforward, and its mathematical
justification is far from being obvious. However, the conclusions we arrive at are
consistent with the results already available in the literature.
In particular, we shall stress the following two points:
- If the (discrete) error-estimating method has order
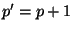 , then the uniform order
of the continuous advancing method should be
, then the uniform order
of the continuous advancing method should be 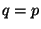 . On the contrary, if
. On the contrary, if 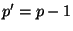 , then
, then
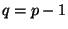 is sufficient.
is sufficient.
- Both the discrete and the uniform local errors should be controlled, rather than the sole
discrete local error as is done in ODE codes. More precisely, the given tolerance
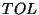 should bound
the discrete local error per unit step and, at the same time, the absolute uniform
local error. To this aim, one can use a continuous error-estimating method of uniform order
should bound
the discrete local error per unit step and, at the same time, the absolute uniform
local error. To this aim, one can use a continuous error-estimating method of uniform order 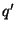 other than
other than 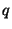 , say
, say 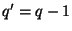 . However, under certain hypotheses on the problem and on the
method, one might be satisfied with controlling the discrete local error only.
. However, under certain hypotheses on the problem and on the
method, one might be satisfied with controlling the discrete local error only.
We shall conclude with some numerical illustrations using the classical explicit 4-stage RK method
of order 4 with suitable continuous extension of uniform order 4.



Next: Bibliography
Ernst Hairer
2002-05-07