6. Annexes
6.1. Traduction des catégories de végétation
Nous indiquons ici les traductions en français des catégories de végétation qui ont été utilisées dans le chapitre 3.3.3. Ces traductions sont indicatives et ont été faites par l'auteur de ce travail.
6.2. Cartes de végétation simplifiée et capacités de soutien
Cette Annexe présente la correspondance entre les catégories de végétation utilisées principalement dans ce travail et les catégories simplifiées (Tableau 6.2.). Ce Tableau indique également les capacités de soutien dérivées pour ces catégories simplifiées, dont la représentation cartographique est présentée dans la Figure 6.1. Ces cartes simplifiées ont été utilisées dans le cadre d'une analyse de sensibilité sur les variables de végétation présentée dans le chapitre 4.6.4.
Les capacités de soutien dérivent des valeurs de Binford (2001) et ont été obtenues en faisant la moyenne des valeurs de chaque catégorie détaillée englobée (trouvées dans le Tableau 3.2).
Pour ces dernières, nous indiquons, entre parenthèses, l'identificateur de catégorie de végétation Adams tel que définit dans le Tableau 3.2. Les valeurs de friction sont celles utilisées dans l'analyse de sensibilité des variables de végétation (voir chapitre 4.6.4).
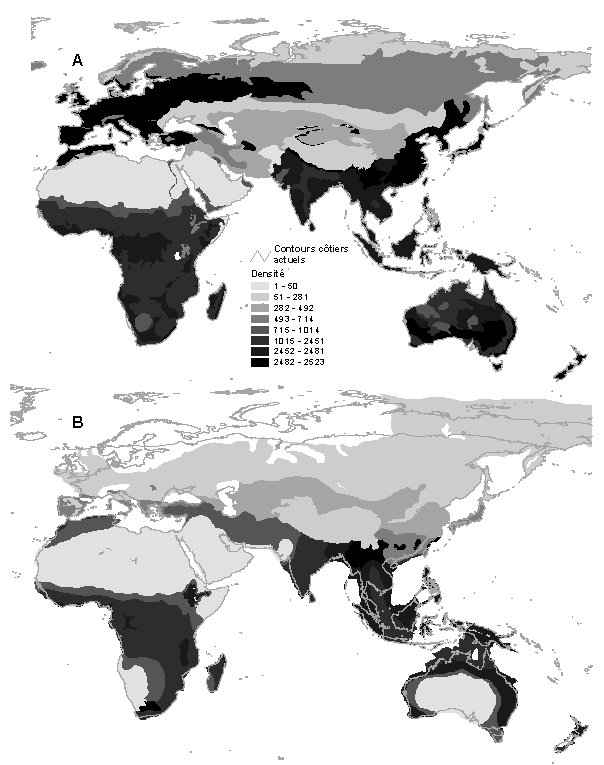
Les contours côtiers actuels sont représentés en traits fins. Les densités sont en nombre de personnes par 10'000 km2.
6.3. Test pour trouver la projection géographique adéquate
Cette Annexe présente la méthodologie et les outils permettant de définir la projection cartographique qui minimise les distorsions sur la surface de l'Ancien Monde. La définition d'une projection géographique et la discussion sur les distorsions dues aux projections ont été présentées au chapitre 4.3.2. Tous les outils discutés dans ce chapitre sont disponibles sur l'Annexe on-line de la thèse sur http://cmpg.unibe.ch/thesis/ray/online_annex.htm.
6.3.1. But et démarche
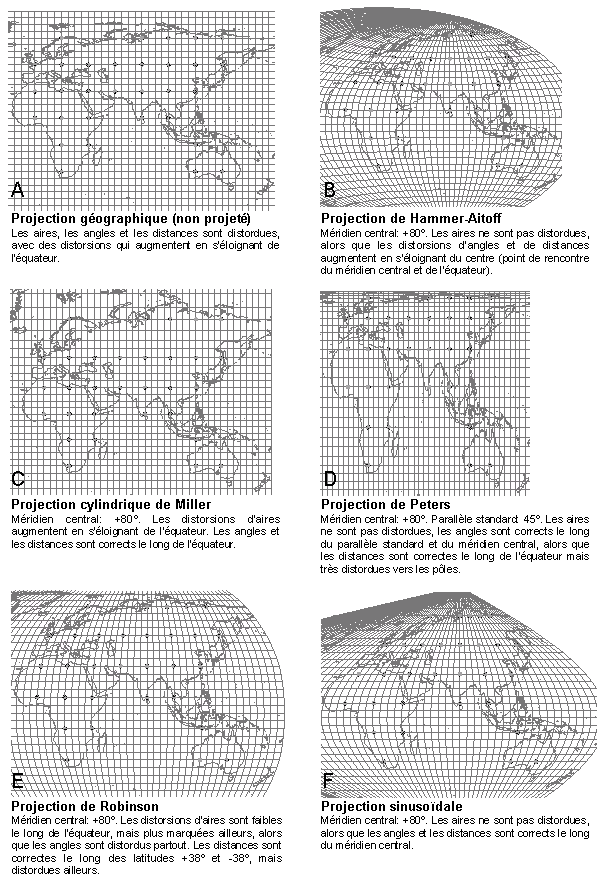
Nous avons retenu cinq projections pour le test. Il s'agit des projections de Hammer-Aitoff (ou plus simplement appelée projection de Hammer), de Miller, de Peters, de Robinson, et de la projection sinusoïdale. Elles sont présentées dans la Figure 6.2., dans laquelle figurent également les caractéristiques de chacune d'entre elles. Les projections utilisées demandent d'attribuer un méridien (longitude) central, le long duquel il y a peu ou pas de distorsions. L'Ancien Monde étant compris entre les longitudes -20º; +180º, nous avons choisi un méridien central fixé à la moitié de la largeur longitudinal de l'Ancien Monde, soit à +80º. Les latitudes et les longitudes sont tracées tous les cinq degrés décimaux et permettent de visualiser les différences entre projections.
Nous avons aussi représenté l'Ancien Monde non projeté dans la Figure 6.2A. Une carte non projetée représente les latitudes et les longitudes régulièrement espacées et parallèles. Cette configuration est par définition la plus distordue.
Le test consiste à calculer, pour chaque projection, une matrice de distances entre 31 points distribués uniformément tous les 20º sur les surfaces continentales (voir Figure 6.2A). Ces matrices de distances vont ensuite être comparées, par un calcul de corrélation, à une matrice de distances géographiques 'vraies'. Ces distances 'vraies' sont calculées à l'aide de la notion de l'arc sphérique, qui est la distance entre deux points sur la surface d'une sphère. Cette distance d'arc est donc la distance géographique correcte séparant deux points sur la Terre, si l'on ne tient pas en compte le relief et que l'on considère la Terre comme sphérique (alors qu'elle est en réalité aplatie aux pôles). Nous avons développé le logiciel GEODIST pour calculer ces distances d'arc. Ce logiciel est présenté dans l'0.
Les matrices de distances pour les cinq cartes projetées se calculent sur la base d'une carte au format raster. En effet, nous voulons une même structure de base que celle utilisée pour les simulations du programme FRICTION. Un moyen efficace de calculer une distance sur une carte raster peut se faire par un chemin de moindre coût (CMC). La définition d'un CMC est trouvée dans l'Annexe 6.3.2. En calculant les CMC entre toutes les paires de points, une matrice de CMC peut alors être obtenue. L'obtention de cette matrice est discutée dans l'Annexe 6.3.3. Pour faciliter le calcul des CMC et l'obtention de la matrice de CMC sur plusieurs cartes, nous avons développé l'extension CostDistanceMatrix pour ARCVIEW 3.x. Cette extension est présentée dans l'3.5.
Les 31 points tests sont répartis tous les 20º.
Une matrice (triangulaire) de distance sur les 31 points utilisés représente 465 distances, et permet de bien couvrir la surface considérée ente les différentes latitudes et longitudes. En comparant les matrices entre elles, mais surtout avec la matrice de distances d'arc, il est alors possible de mettre en évidence la magnitude des distorsions de distance dues à la projection. Cette comparaison de matrice se fait par le calcul de la corrélation entre deux matrices, dont la significativité est calculée par le test de Mantel présenté dans l'Annexe 6.3.6.
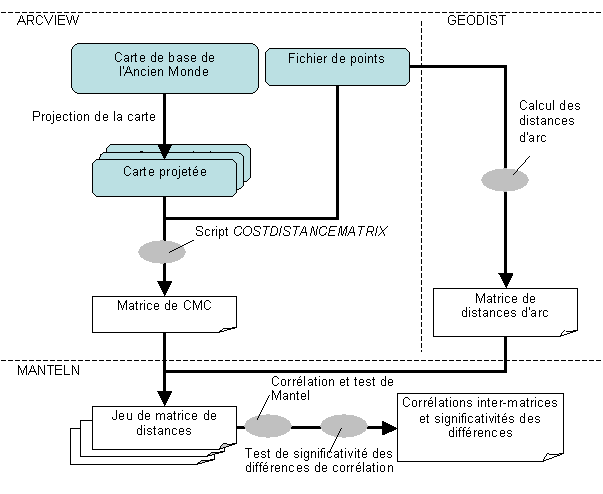
Les encadrés blancs sont des fichiers textes, et les encadrés pleins sont des fichiers SIG de ARCVIEW. Les dernières étapes se font dans le logiciel MANTELN. Les ovales représentent des étapes de calcul particulières.
La projection possédant le moins de distorsion est alors celle dont la corrélation avec la matrice de distances d'arc est la plus grande. Une forte corrélation indique en effet que les valeurs des distances projetées en deux dimensions approchent les 'vraies' valeurs obtenues sur la sphère. Nous verrons que les corrélations obtenues sont très fortes et que certaines ne sont pas très différentes entre elles. Dans cette situation, il est important de pouvoir tester si deux corrélations sont statistiquement différentes. Un tel test n'a pas été trouvé dans la littérature, et nous avons décidé de développer notre propre méthode statistique, qui est présentée dans l'Annexe 6.3.7.
Pour permettre une utilisation optimisée du calcul des corrélations, du test de Mantel, et du test des différences entre corrélations, nous avons développé un programme qui rassemble tous ces outils statistiques. Ce programme, appelé MANTELN, est présenté dans l'Annexe 6.3.8.
Le schéma des étapes nécessaires aux calculs des corrélations entre les matrices de distances est présenté dans la Figure 6.3. Tous les outils présentés dans cette Annexe présentent un intérêt qui va plus loin que le test de la projection adéquate. De nombreux chercheurs ont déjà utilisé nos outils pour calculer des matrices de CMC entre des populations. Ces outils ont pu être utilisés avec succès notamment pour des calculs de distances entre habitats forestiers et aquatiques de plusieurs espèces d'amphibiens (Abdelhak, 2002; Cohas, 2002), ainsi que pour une comparaison entre CMC et distances génétiques chez une espèce de salamandre. Pour ce dernier travail, la référence provisoire de l'article en préparation est
Thompson, M. D., Ray, N. et Russell, A. P. in prep. Contrasting neutral and non-neutral mitochondrial genes from Long-toed salamander (Ambystoma macrodactylum) populations: using GIS cost-path distances to spatially examine clades in Cordilleran glacial valleys.
6.3.2. Calcul des distances géographiques par le programme GEODIST
Le calcul des distances géographiques est basé sur la notion d'arc sphérique, qui est la distance entre deux points sur une sphère. Cette distance (en kilomètre) est calculée par  où a est la latitude et b la longitude en degrés décimaux (les indices 1 et 2 représentant les deux coordonnées du point 1 et du point 2), et r est le rayon de la Terre (fixé à 6367 km). Une discussion détaillée sur l'équation utilisée peut être trouvée sur http://www.mathforum.com/library/drmath/view/51711.html
où a est la latitude et b la longitude en degrés décimaux (les indices 1 et 2 représentant les deux coordonnées du point 1 et du point 2), et r est le rayon de la Terre (fixé à 6367 km). Une discussion détaillée sur l'équation utilisée peut être trouvée sur http://www.mathforum.com/library/drmath/view/51711.html
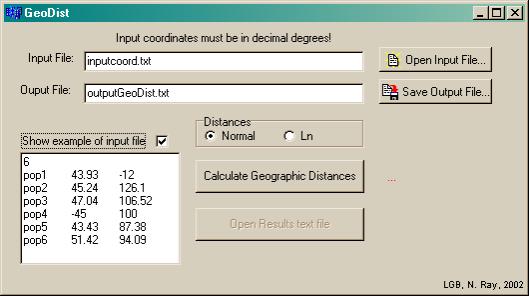
Nous avons développé le programme GEODIST pour calculer ces distances d'arc entre un jeu de points. L'interface utilisateur (Figure 6.4) permet de choisir un fichier d'entrée, dont le format est indiqué dans la fenêtre Show example of input file. La première ligne de ce fichier est le nombre de point considéré. Chaque ligne suivante est constituée d'un identificateur de point (chaîne de caractère), suivi de la latitude et de la longitude du point en degrés décimaux. Le fichier de sortie est une matrice de distances géographiques en kilomètres entre tous les points d'entrée.
Il est également possible de sortir une matrice des logarithmes naturels des distances. Pour cette dernière, lorsque la distance est nulle, la valeur de sortie est également nulle. Les distances calculées ne prennent pas en compte l'aplatissement de la sphère terrestre aux pôles.
6.3.3. Définition d'un chemin de moindre coût (CMC)
Un des problèmes intéressants que peut aider à résoudre un SIG est de trouver le chemin le plus rapide (ou le plus court) entre un ou plusieurs points de départ et un point d'arrivée. Le problème peut être discuté dans le contexte d'un réseau, tel que celui des routes ou des lignes électriques. Le chemin de moindre coût (CMC) est alors celui dont la somme des longueurs des tronçons, le long du réseau, est la plus petite. Il est également possible de calculer un chemin de moindre coût sur une surface continue, représentée en format raster. Cette surface doit alors indiquer, pour chacune de ses cellules (ou pixels), le coût de passage (en temps ou en énergie). Ces cartes de coût sont plus généralement appelées cartes de friction.
Sur la base d'une carte de friction, et d'un ou de plusieurs point de référence définis arbitrairement, il est possible de calculer une carte de coût cumulé (accumulative cost), dont la valeur en chaque point représente le coût minimum de déplacement entre ce point et le ou les points de référence. On peut se représenter cette carte comme une carte hypsométrique dont l'altitude en chaque point est le coût cumulé, et où le point le plus 'bas' est le point de référence. Le CMC de n'importe quel point au point de référence est alors défini comme le chemin le plus court suivant le gradient de 'pente' de la carte de coût cumulé. Cette démarche de calcul est analogue à celle consistant, en hydrologie, à trouver les bassins versants sur la base d'un modèle numérique d'altitude.
Les CMC trouvent nombre d'applications en économie, où ceux-ci sont par exemple généralisés pour tenir en compte de manière complexe des coûts de voyage associés à certains tronçons (Huriot et al., 1989). Des applications des CMC sont aussi trouvées en écologie, par exemple pour déterminer des passages préférentiels de mouvements (Walker et Craighead, 1997; Purves et Doering, 1999), pour déterminer la connectivité biologique entre habitats ou populations (Villalba et al., 1998; Ray, 1999; Ray et al., 2002), pour optimiser la visibilité ou le couvert de chemins pédestres (Lee et Stucky, 1998), ou plus récemment pour comparer des distances environnementales avec des distances génétiques (Thompson et al., in prep). En archéologie et en anthropologie, des approches par CMC sont utilisées lorsque des anciens chemins sont recherchés à l'échelle régionale (voir par exemple Bellavia, 2001). La friction est alors dérivée uniquement à partir du relief qui, à cette échelle, peut être représenté de manière relativement fine. A l'échelle continentale des Amériques, plusieurs études ont dérivé des cartes de coût cumulé pour modéliser les temps d'arrivées des premiers colonisateurs en fonction de l'hétérogénéité des habitats potentiels (Steele et al., 1995; Glass et al., 1997; Steele et al., 1998), ou même pour déterminer les chemins préférentiels empruntés lors de la colonisation (Anderson et Gillam, 2000). Les résultats de ces applications sont attrayants, bien que dépendant tous d'estimation de coût de déplacement qui sont parfois très subjectifs.

Les 31 points sont projetés dans la projection Hammer-Aitoff, avec les mêmes paramètres que dans la Figure 6.2.
Les outils permettant les calculs de CMC sont maintenant bien implémentés dans la grande majorité des logiciels SIG. Nous avons utilisé pour ce travail les fonctions Costdistance et Costpath 41 du logiciel ARCVIEW 3.1. Ces fonctions sont basées sur l'algorithme de Zhan et al. (1993), qui est un algorithme optimisé à partir des algorithmes de Dijkstra (1959) et de Bellman (1958). Nous n'allons pas ici détailler cet algorithme, car il est très bien expliqué graphiquement dans l'aide en ligne de ARCVIEW (ESRI, 1998). La Figure 6.5. montre un exemple de chemins de moindre coût obtenus avec la matrice de points discutée dans l'Annexe3.1, projetée dans la projection Hammer-Aitoff. La carte de friction sous-jacente utilisée est uniforme (chaque cellule a le même coût).
Un désavantage implicite des calculs en mode raster est la représentation en 'escalier' d'un CMC. Pour nous représenter ce phénomène, nous pouvons considérer le chemin de moindre coût entre deux points distincts sur une surface homogène. En espace continu ce chemin est, selon les propriétés de l'espace euclidien, une ligne droite reliant les deux points. En espace discrétisé par contre, le chemin rencontre des contraintes spatiales dues à la résolution du grid. Nous constatons ce phénomène en observant la Figure 6.5, où l'on remarque que les CMC ne sont pas du tout représentés en lignes droites, et que des effets d'escalier apparaissent dus à la structure du grid sous-jacent. Ce phénomène est connu, et il a été montré que les directions prises par les CMC dans des surfaces homogènes dépendent de l'algorithme utilisé (Wagner et al., 1993; Douglas, 1994), et que des représentations différentes apparaissent alors selon le logiciel SIG utilisé. En effet, un CMC n'est pas forcément unique, il peut exister plusieurs chemins alternatifs qui représenteront tous la même distance minimum.
6.3.4. Calcul d'une matrice de chemins de moindre coût
Une matrice de chemins de moindre coût représente les distances de CMC entre toutes les paires de point distinctes d'un jeu de points. Cette matrice a donc la même configuration qu'une matrice de distances d'arc géographique obtenue par le logiciel GEODIST.
Jeux de points
Le premier fichier nécessaire pour le calcul de la matrice est un fichier de point. Pour les applications en écologie ou en génétique, chaque point représente généralement l'emplacement d'une population. Les coordonnées des points sont généralement dérivées des données de la littérature pour les populations en question. Lorsque la localisation géographique d'une population n'est connue que par un nom de lieu, il est possible d'utiliser des bases de données on-line telle que le GNS (GEOnet Names Server 42 ) ou le TGN (Thesaurus of Geographic Names 43 ) pour trouver les coordonnées des longitudes et des latitudes. Il est important de travailler avec des coordonnées en degrés décimaux, de sorte que les points puissent être correctement projetés quelle que soit la projection utilisée pour les grids des cartes de friction. Il est possible de travailler avec un fichier de polygones (appelés régions) au lieu du fichier de points. Les CMC sont alors calculés à partir du bord de ces régions.
L'utilisation d'un fichier de point dans ARCVIEW nécessite son importation au format shapefile. Ce format est un format standard et ouvert 44 . Cette importation est aisée, et peut se faire par exemple à partir d'un fichier EXCEL sauvé au format DBF.
Obtention d'une matrice de CMC
Le deuxième fichier nécessaire est la carte de friction, qui définit le coût de chaque pixel. Pour le test sur les projections, nous travaillons avec une carte de friction uniforme (le coût de tous les pixels est égal à 1) et rectangulaire. Nous ne considérons pas les contours des continents pour la simple raison que la méthode des arcs ne peut s'appliquer que sur une sphère et ne peut pas prendre en compte les contours continentaux. De manière plus générale, une carte de friction peut être hétérogène, avec des coûts de friction qui sont déterminés par des contraintes environnementales comme le relief ou la végétation. La carte de friction doit être au format grid d'ARCVIEW.
Une fois les données de base rassemblées et formatées de manière adéquate, la matrice de CMC entre paires de point peut être calculée. Cette matrice est similaire à une matrice de distances géographiques, mais contiendra les coûts cumulés de migration entre chaque paire de points. Le coût cumulé entre un point A et un point B est obtenu en identifiant la valeur de la carte de coût cumulé (avec une expansion au départ de A) au point B. Ce coût cumulé peut être obtenu également en sommant les valeurs de friction des cellules le long du CMC. La matrice de distances de coût est triangulaire puisque nous ne travaillons qu'avec des frictions isotropiques impliquant que le CMC de A à B est égale au CMC de B à A. Les étapes du processus itératif permettant d'obtenir une matrice de distances de coût peuvent être résumées de la façon suivante:
- Le premier point de la grille est défini comme source, les n -1 points restants étant les cibles;
- Une carte de coût cumulé est calculée à partir du point source;
- Les coûts pour atteindre chacun des n -1 cibles sont enregistrés dans la matrice;
- Définition du point suivant comme source, et reprise au point 2 jusqu'à ce que tous les points aient été parcourus.
6.3.5. Extension ARCVIEW CostDistanceMatrix
Cette extension pour ARCVIEW 3.x permet de calculer des matrices de CMC entre un nombre arbitraire de points ou de polygones, et sur la base d'une ou de plusieurs cartes de friction. L'extension est écrite dans le langage de script Avenue de ARCVIEW. Le mécanisme a été rendu indépendant de la projection utilisée pour les cartes de friction. Pour cela, il faut que le fichier de points ne soit pas projeté 45 et les coordonnées des points soient en degrés décimaux.
Deux scripts forment le corps de cette extension. Le premier, CostDistanceMatrixMultiGrid, permet de choisir les cartes de friction et appelle de manière itérative le deuxième script CostDistanceMatrix qui contient les fonctions principales de calculs. Seul ce dernier script est appelé lorsque les calculs ne sont demandés que sur une seule carte de friction. Pour une explication détaillée de la façon de traiter les distances lorsque des polygones sont utilisés, se reporter à l'aide en ligne de ARCVIEW (ESRI, 1998).
Lorsque l'extension est chargée, un nouveau menu apparaît, appelé 'Cost distance matrix' (Figure 6.6.). Il possède deux sous-menus permettant le calcul sur un ou plusieurs grids

Après le choix d'un sous-menu, plusieurs informations vont être demandées à l'utilisateur:
- Choix du fichier de points ou de polygones utilisé comme éléments sources pour le calcul des coûts accumulatifs. Si une sélection d'un ou plusieurs éléments a été faite dans le fichier avant de lancer les calculs, seuls les éléments sélectionnés seront utilisés;
- Choix des cartes de friction (grids) si l'analyse multi-grids est choisie. Le grid actif dans la vue est choisi automatiquement si l'analyse sur un grid est choisie;
- Choix du coût accumulatif maximum. Le processus de calcul de la carte de coût cumulé s'arrête lorsque ce coût est atteint. Le champ est laissé blanc si l'on désire ne pas mettre de contraintes sur ce coût, ce qui est généralement recommandé;
- Choix du nom du fichier de sortie des résultats, sous la forme d'une table au format dbf.
- Choix de sauver individuellement chaque carte de coût accumulatif (une par point source). Cela peut être utile, entre autres, pour vérifier l'étendue de la carte lorsqu'un coût accumulatif maximum a été défini au point 3.
Dans le code Avenue, deux variables booléennes (flags) permettent de plus de contrôler les matrices de sortie:
_DiagonalMatrix_: true (matrice de sortie diagonale) ou false (matrice de sortie carrée)
_TextOutput_: true (matrices de sortie au format dbf et au format txt) ou false (matrices de sortie au format dbf)
Il faut recompiler l'extension si un changement est fait sur une de ces variables booléennes.
Il est possible qu'un élément (point ou polygone) ne soit pas atteint par l'extension de la carte de coût cumulé, soit parce que le coût cumulé maximum a été mis à une valeur trop faible, soit parce que l'élément en question se trouve dans une zone de friction infinie (ou valeur No Data dans ARCVIEW). Dans ce cas, le CMC prend la valeur -1 dans la matrice de sortie.
Cette extension est téléchargeable sur le site on-line de la thèse. Elle a également été publiée sur le site d'ESRI sur http://arcscripts.esri.com/details.asp?dbid=7289769
http://www.unige.ch/cyberdocuments/theses2003/RayN/images/Ray_cost.pdf
6.3.6. Test de Mantel
Les corrélations entre les matrices et leurs significativités sont calculées par le test de correspondance matricielle classique de Mantel (1967; Smouse et al., 1986), brièvement décrit ci-dessous. Nous traitons premièrement le cas de deux matrices.
Soit deux matrices 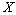 et
et  de taille
de taille  , nous calculons la statistique
, nous calculons la statistique 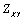 par
par
 |
(6.1) |
qui mesure l'association des éléments des deux matrices considérées. La valeur observée de  est ensuite comparée à la distribution des valeurs de
est ensuite comparée à la distribution des valeurs de 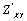 calculée lorsque l'association entre les deux matrices est perturbée. Pour cela, nous procédons à des permutations des lignes et colonne correspondantes d'une des matrices tout en conservant l'autre constante.
calculée lorsque l'association entre les deux matrices est perturbée. Pour cela, nous procédons à des permutations des lignes et colonne correspondantes d'une des matrices tout en conservant l'autre constante. 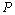 est recalculée après chaque permutation, pour générer sa distribution empirique sous l'hypothèse nulle d'absence de corrélation. La probabilité empirique
est recalculée après chaque permutation, pour générer sa distribution empirique sous l'hypothèse nulle d'absence de corrélation. La probabilité empirique 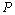 (p value) associée à
(p value) associée à  d'observer une valeur inférieure ou égale à
d'observer une valeur inférieure ou égale à  est alors
est alors
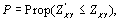 |
(6.2) |
La statistique  peut être transformée en un coefficient de corrélation par
peut être transformée en un coefficient de corrélation par
 |
(6.3) |
où 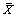 et
et 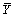 sont les moyennes de tous les éléments d'une matrice.
sont les moyennes de tous les éléments d'une matrice.
Le test de Mantel a été modifié et étendu à trois matrices par Smouse et al. (1986) et Smouse (1992) afin de pouvoir calculer des corrélations partielles. Dans ce test de Mantel partiel, deux matrices de distances  et
et  sont alors utilisées pour prédire les éléments d'une matrice indépendante
sont alors utilisées pour prédire les éléments d'une matrice indépendante 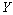 . Les coefficients de corrélation partielle sont donnés par
. Les coefficients de corrélation partielle sont donnés par
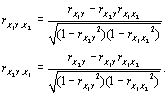 |
(6.4) |
Le test de significativité des corrélations partielles est réalisé en permutant aléatoirement la matrice 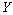 , en conservant les matrices
, en conservant les matrices 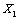 et
et  constantes, et en recalculant à chaque permutation la statistique d'intérêt.
constantes, et en recalculant à chaque permutation la statistique d'intérêt.
Ce test étendu permet de traiter de manière adéquate l'autocorrélation inhérente aux matrices de distances, et il a été utilisé abondement pour comparer simultanément des matrices géographiques, génétiques et culturelles (voir par ex., Excoffier et al., 1991; Barbujani et al., 1995; Sokal et al., 1997; Dupanloup de Ceuninck, 1999; Eller, 1999; Rosser et al., 2000; Sokal et al., 2000).
6.3.7. Test de significativité des différences de corrélation
Si le test de Mantel permet de tester la significativité d'une corrélation, il n'est pas possible de l'utiliser pour tester la significativité de la différence entre deux corrélations. Aucun test du genre n'ayant pu être trouvé dans la littérature, nous avons collaboré avec la Professeur Peter Smouse (Rutgers University, USA) afin d'implémenter une méthodologie de test adéquate.
Le but de cette collaboration était d'aboutir à une méthodologie générale permettant la comparaison de deux corrélations, quelles que soient les identités des deux paires de matrices utilisées pour calculer ces corrélations. Autrement dit, la méthode recherchée aurait dû permettre d'aboutir à un test robuste si les quatre matrices étaient différentes ou si deux des quatre matrices étaient identiques. Ce dernier cas est celui rencontré pour la problématique principale qui nous intéresse dans cette Annexe, puisque nous voulons comparer une corrélation obtenue entre une matrice de distances d'arc et une matrice de CMC dans une projection A, avec une corrélation obtenue entre cette même matrice de distances d'arc et une matrice de CMC dans une projection B. Une autre application fréquemment demandée par notre laboratoire est de pouvoir comparer, par exemple, les corrélations obtenues entre une matrice de distances génétiques et deux matrices alternatives de distances linguistiques ou géographiques. Si une de ces corrélations est plus haute que l'autre, ce qui arrive fréquemment, il est alors important de pouvoir affirmer si elle est, ou non, significativement plus haute.
Il s'est finalement avéré qu'une méthode générale n'était pas triviale, et nous avons préféré nous concentrer sur l'implémentation d'une méthode permettant la comparaison des corrélations lorsqu'une matrice identique est partagée entre les deux corrélations. Cette méthode est décrite ci-dessous.
La corrélation  entre deux matrices
entre deux matrices 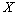 et
et 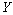 est calculée par le coefficient de Pearson (Sokal et Rohlf, 1981, p. 565) selon
est calculée par le coefficient de Pearson (Sokal et Rohlf, 1981, p. 565) selon
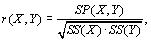 |
(6.5) |
où  est la somme des produits des éléments correspondants entre les deux matrices, et
est la somme des produits des éléments correspondants entre les deux matrices, et 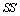 est la somme des carrés des éléments d'une matrice.
est la somme des carrés des éléments d'une matrice.
Notons  la corrélation entre une paire de matrices de distances
la corrélation entre une paire de matrices de distances  et
et 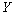 , et
, et  la corrélation entre une autre paire de matrices de distances
la corrélation entre une autre paire de matrices de distances 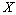 et
et  . La matrice
. La matrice  est donc la matrice commune aux deux corrélations. Une idée de base était d'utiliser une distribution nulle des différences
est donc la matrice commune aux deux corrélations. Une idée de base était d'utiliser une distribution nulle des différences 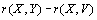 en permutant une des matrices de chaque paire de manière similaire au test de Mantel. La difficulté de cette procédure est qu'au cours des répétitions de permutation, elle réduit les corrélations moyennes
en permutant une des matrices de chaque paire de manière similaire au test de Mantel. La difficulté de cette procédure est qu'au cours des répétitions de permutation, elle réduit les corrélations moyennes 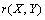 et
et 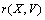 , en les faisant tendre vers zéro. Nous ne voulons pas ce comportement, mais plutôt une implémentation des permutations qui permette que les corrélations restent positives.
, en les faisant tendre vers zéro. Nous ne voulons pas ce comportement, mais plutôt une implémentation des permutations qui permette que les corrélations restent positives.
Pour ce faire, il convient premièrement d'ajuster les matrices à la même échelle. Dans le schéma classique du test de Mantel, 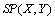 change au cours des permutations, alors que
change au cours des permutations, alors que  et
et  sont invariants. Le dénominateur de l'équation (1.5) indique alors en quelque sorte l'échelle de la mesure. Prenons maintenant une matrice
sont invariants. Le dénominateur de l'équation (1.5) indique alors en quelque sorte l'échelle de la mesure. Prenons maintenant une matrice 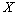 et multiplions chacun de ses éléments par une même constante
et multiplions chacun de ses éléments par une même constante  , où
, où  est la somme des éléments individuels de la matrice
est la somme des éléments individuels de la matrice 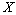 . La somme des carrés
. La somme des carrés  de cette nouvelle matrice altérée
de cette nouvelle matrice altérée 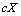 est égale à 1 par construction. De manière similaire nous obtenons la somme des carrés
est égale à 1 par construction. De manière similaire nous obtenons la somme des carrés 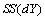 d'une matrice altérée
d'une matrice altérée  , où
, où 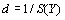 . Si nous calculons maintenant
. Si nous calculons maintenant 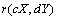 , nous obtenons
, nous obtenons 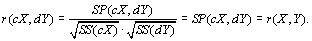 .
.
Nous avons donc changé l'échelle sans changer les caractéristiques des matrices. Nous pouvons appliquer le même traitement à la paire de matrices 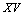 de sorte que
de sorte que  où
où 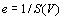 .
.
La moyenne  des deux corrélations peut alors s'écrire
des deux corrélations peut alors s'écrire  .
.
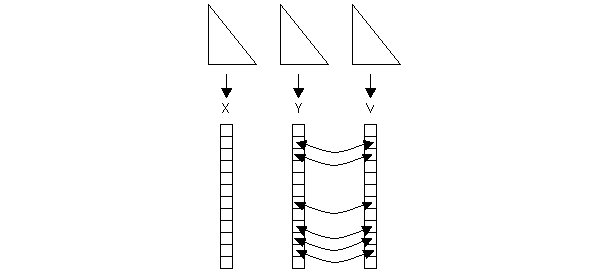
Les triangles représentent les matrices diagonales de distance, qui sont d'abord linéarisées sous la forme d'un vecteur. Les échanges entre Y et V se produisent avec une probabilité de 0.5 pour chaque paire d'éléments correspondants entre les deux matrices.
Concernant l'étape des permutations, nous ne permutons pas les lignes et colonnes selon le schéma classique de Mantel. Nous procédons à la place à des permutations inter-matrices d'éléments correspondants (processus illustré à la Figure 6.7). En maintenant 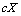 constant, nous prenons les éléments correspondants de
constant, nous prenons les éléments correspondants de 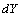 et
et  , et nous les permutons aléatoirement de la façon suivante: le ijème élément de
, et nous les permutons aléatoirement de la façon suivante: le ijème élément de  forme une paire avec le ijème élément de
forme une paire avec le ijème élément de 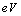 , et avec une probabilité de 0.5 ces deux éléments sont échangés entre les deux matrices. Puisque nous travaillons avec des matrices de distances symétriques, le même traitement est appliqué à chaque fois au jième élément. Un événement de permutation consiste donc à parcourir tous les éléments sous la diagonale de la matrice et à leur appliquer l'échange (swap) inter-matrice avec la probabilité de 0.5.
, et avec une probabilité de 0.5 ces deux éléments sont échangés entre les deux matrices. Puisque nous travaillons avec des matrices de distances symétriques, le même traitement est appliqué à chaque fois au jième élément. Un événement de permutation consiste donc à parcourir tous les éléments sous la diagonale de la matrice et à leur appliquer l'échange (swap) inter-matrice avec la probabilité de 0.5.
Avec ce traitement particulier des permutations, les éléments des matrices sont perturbés de façon à ce que 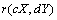 et
et  puissent varier, mais que
puissent varier, mais que 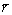 reste invariant. Notre hypothèse nulle est que la différence entre les corrélations issues des deux paires de matrice soit égale à zéro (
reste invariant. Notre hypothèse nulle est que la différence entre les corrélations issues des deux paires de matrice soit égale à zéro (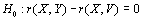 ). Il nous reste à définir une statistique de test qui sera évaluée à chaque permutation. Nous pouvons simplement choisir comme statistique la différence entre les deux corrélations obtenues par les matrices perturbées, soit
). Il nous reste à définir une statistique de test qui sera évaluée à chaque permutation. Nous pouvons simplement choisir comme statistique la différence entre les deux corrélations obtenues par les matrices perturbées, soit 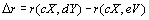 . En procédant à un nombre élevé d'événements de permutations (typiquement 10'000), et en recalculant à chaque fois les corrélations, nous obtenons alors une distribution nulle de la statistique de test
. En procédant à un nombre élevé d'événements de permutations (typiquement 10'000), et en recalculant à chaque fois les corrélations, nous obtenons alors une distribution nulle de la statistique de test  . La significativité (p value) de la différence entre nos deux paires de matrice est alors le nombre de fois sur
. La significativité (p value) de la différence entre nos deux paires de matrice est alors le nombre de fois sur  que
que 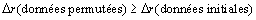 . Si
. Si 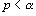 , où
, où  est le seuil de significativité (typiquement 0.05), nous rejetons
est le seuil de significativité (typiquement 0.05), nous rejetons  et considérons que nos deux corrélations sont significativement différentes.
et considérons que nos deux corrélations sont significativement différentes.
6.3.8. Programme MANTELN
Les corrélations entre matrices, les tests de Mantel, et les tests de significativité des différences de corrélation doivent souvent être fait sur un grand nombre de matrices de distances (géographiques, CMC ou génétiques). Il est alors intéressant d'avoir à disposition un programme qui puisse faire ces calculs sur un nombre arbitraire de matrices. Nous avons pour cela développé en C++ le programme MANTELN, qui utilise une partie du code du programme MANTEL (Laurent Excoffier, LGB).
Ce programme implémente les tests statistiques discutés dans les deux Annexes précédentes. Ce programme est en ligne de commande, et peut prendre jusqu'à trois paramètres, suivant la synopsis suivante:
Manteln [fichier d'entrée] ([nombre de permutation] [significativité des différences de corrélation])
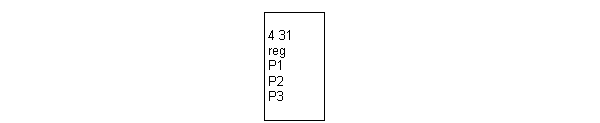
fichier d'entrée: nom (avec extension) du fichier texte décrivant le nombre, la taille et les noms des matrices sur lesquelles doivent être fait les calculs. La première ligne du fichier contient le nombre de matrices considérées, suivi de la taille des matrices (cette taille est le nombre de ligne ou de colonne, puisque nous travaillons avec des matrices carrées). Les lignes qui suivent sont les noms des fichiers texte contenant chacun une matrice. Ces fichiers doivent avoir l'extension '.dis', et cette extension ne doit pas être indiquée dans le fichier d'entrée. Un exemple de fichier d'entrée est trouvé ci-dessous, dans lequel quatre matrices de 31 lignes par 31 colonnes sont définies:
nombre de permutation: ce paramètre facultatif indique le nombre de permutations utilisées pour le test de significativité d'une corrélation, ainsi que pour le test de significativité de la différence entre deux corrélations. La valeur par défaut, utilisée lorsque ce paramètre n'est pas défini, est de 10'000.
significativité des différences de corrélation: ce paramètre facultatif est un booléen. Sa valeur doit être mis à 1 si l'on veut que le calcul des significativités des corrélations se fasse seulement entre les paires de matrice qui ont comme matrice commune la première matrice définie dans le fichier d'entrée ('reg' dans l'exemple ci-dessus). Ce choix permet de grandement minimiser les temps de calcul, lorsque l'on est seulement intéressé aux comparaisons de matrice impliquant une matrice en particulier (comme c'est le cas pour le test des projections cartographiques). La valeur par défaut de ce paramètre est 0, et le test de significativité de corrélation se calcule alors entre toutes les paires de matrices qui possèdent une matrice en commun.
Les fichiers de sorties du programme MANTELN sont au nombre de cinq, et sont tous sous une forme matricielle:
|
correl.txt : comprend les corrélations entre les matrices correl_pvalues.txt : comprend les significativités (p values) des corrélations de correl.txt partial_corel.txt : comprend les corrélations partielles entre les matrices, en utilisant la première matrice dans le fichier d'entrée ('reg' dans l'exemple ci-dessus) comme matrice indépendante. partial_corel_pvalues.txt : comprend les significativités (p values) des corrélations partielles de partial_corel.txt. diff_corel_pvalues.txt : comprend les significativités (p values) des différences de corrélation entre les paires de matrice. Si le paramètre significativité des différences de corrélation est à 0, il y a certaines paires de corrélation qui ne partagent pas de matrice commune, et pour lesquelles nous ne calculons donc pas la significativité des différences de corrélation. Pour ces cas, le caractère '-' apparaît dans la matrice de résultats. |
Par ajout d'une option de compilation (_LN_TRANSFORM_) dans le code source du programme, nous obtenons le programme LOGDIST qui transforme toutes les valeurs des matrices de distances en leurs logarithmes naturels. Ce programme prend le même fichier d'entrée indiquant les n matrices à transformer et donne n fichiers en sortie, dont les noms sont ln_*.dis, où * est à remplacer par le nom de base des matrices d'entrée.
6.3.9. Résultats du test
Les corrélations entre nos sept matrices (matrice de CMC pour chacune des cinq projections, une matrice de CMC non-projetée et la matrice des distances d'arc géographique) sont présentées dans le Tableau 6.3.A. Nous avons également procédé au test des différences entre les paires de matrice qui comportaient la matrice des distances d'arc (Arc géo.). Les significativités de ces différences sont présentées dans le Tableau 6.3.B et seront discutées par rapport au seuil de significativité 5%.
Plusieurs résultats peuvent être tirés des Tableaux 6.3.A et 6.3.B :
- La très haute corrélation entre la matrice en projection de Miller et la matrice non projetée (r=0.9930) montre le peu de différences entre ces deux configurations. Les corrélations obtenues entre ces deux matrices et la matrice de distances d'arc ne sont d'ailleurs pas significativement différentes (p=0.4042). Une différence significative pourrait néanmoins être attendue si les points considérés étaient situés majoritairement aux hautes et basses latitudes, puisque c'est spécifiquement dans ces zones que la projection de Miller diffère de la projection géographique.
- Les quatre autres matrices (Peters, Hammer, Robinson, et sinusoïdale) donnent des corrélations avec la matrice de distances d'arc significativement plus grandes (p<0.0001) que la matrice non projetée. Cela indique bien qu'une carte non projetée possède les plus fortes distorsions.
- Les deux projections les moins distordues sont la projection de Hammer et la projection sinusoïdale. Elles ont toutes deux une corrélation avec la matrice de distances d'arc qui est significativement plus élevée (p<0.0001) que les autres projections, mais leurs corrélations avec les distances d'arc (respectivement 0.9784 et 0.9771) ne sont pas statistiquement différentes entre elles au seuil 5% (p=0.0758). L'une ou l'autre peut donc être choisie pour nos simulations, et nous allons utiliser la projection de Hammer.
-
Un moyen d'estimer le pourcentage moyen d'erreur (résidu) dû à l'utilisation d'une projection biaisée peut être calculé par
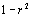 . Ces estimations, pour chacune des projections, se trouvent dans la première ligne du Tabl. 6.3.a. On remarque que l'erreur imputée à une carte non projetée est de 19.0%, ce qui est élevé. Cette erreur est estimée à seulement 4.3% pour la projection de Hammer.
. Ces estimations, pour chacune des projections, se trouvent dans la première ligne du Tabl. 6.3.a. On remarque que l'erreur imputée à une carte non projetée est de 19.0%, ce qui est élevé. Cette erreur est estimée à seulement 4.3% pour la projection de Hammer.
Cette étude sur les projections nous a donc permis de quantifier les distorsions pour chacune des projections retenues. Au vu de l'estimation de l'erreur pour une carte non projetée, nous nous sommes également rendu compte de l'importance du choix d'une projection adéquate. En utilisant la projection de Hammer dans nos simulations sur l'Ancien Monde, nous allons donc minimiser ces distorsions. Ces résultats suggèrent également que lors d'une démarche d'estimation des paramètres d'un modèle de dispersion (par exemple par rapport aux temps d'arrivée à certaines localisations), il est primordial de connaître le biais introduit par la projection utilisée, ceci afin de pouvoir évaluer au mieux l'incertitude autour des valeurs estimées des paramètres.
6.4. Programme FRICTION - aspects techniques
Cette Annexe contient certains aspects techniques du programme FRICTION.
6.4.1 Module d'entrées-sorties
Le module d'entrées-sorties regroupe l'ensemble du flot d'informations entrant et sortant de FRICTION. Il a été discuté de manière générale dans le chapitre 4.3.3. Nous discutons ici de quelques aspects techniques liés à ce module.
Programmes GRID2TEXT et TEXT2GRID
Le programme GRID2TEXT a été développé afin de pouvoir transformer chaque grid en format texte simple qui est ensuite lu dans FRICTION. Il utilise la libraire API gridio de ESRI afin d'accéder directement à la structure du grid. La contrainte de l'utilisation de cette libraire est le fait qu'ARCVIEW doit être installé sur la machine où GRID2TEXT est utilisé. Le programme TEXT2GRID a été réalisé de manière similaire et permet d'écrire un grid à partir d'un fichier texte exporté par FRICTION. La structure des fichiers textes obtenus via GRID2TEXT est une simple matrice de valeurs, sans en-tête, dont les nombres de lignes et de colonnes sont égaux à ceux des grids dans ARCVIEW. Un fichier supplémentaire (header), contenant l'information de géoréférencement des fichiers, est également produit par GRID2TEXT. Ce fichier comprend neuf lignes qui sont :
|
Taille de la cellule (en unités de projection) Nombre de cellule x du block tampon (utilisé pour lire et écrire) Nombre de cellule y du block tampon (utilisé pour lire et écrire) Coordonnée x du centre de la cellule en bas à droite Coordonnée y du centre de la cellule en bas à droite Coordonnée x du centre de la cellule en haut à gauche Coordonnée y du centre de la cellule en bas à gauche Nombre de lignes Nombre de colonnes |
Fonction BuildWorld
Trois fonctions principales constituent le corps de FRICTION. La fonction BuildWorld englobe une série de fonctions qui permettent de construire et d'initialiser un monde virtuel, grâce aux nombreux fichiers et paramètres d'entrée. Le Tabl donne les descriptions des fonctions appelées par BuildWorld. Les deux autres fonctions principales, SimulateDemography et SimulateGenetics, permettent respectivement une simulation démographique (voir chapitre 4.3.4.) et une (ou plusieurs) simulation génétique (voir chapitre 4.3.5.).
L'ordre de ces fonctions dans le tableau correspond à l'ordre successif d'appel dans la fonction BuildWorld.
6.4.2. Module démographique
Le module démographique du programme FRICTION permet de simuler la démographie locale des cellules, ainsi que les migrations entre les cellules. Ce module a été discuté de façon plus générale dans le chapitre 4.3.4. Nous présentons ici les différentes structures d'objet C++ qui ont été implémentées pour réaliser ce module.
Structures des objets implémentés
La Figure 6.8. présente les objets principaux de la structure démographique, ainsi que les relations entre ceux-ci. L'objet World est la structure de base rassemblant les objets et les routines utilisées pour simuler et pour stocker l'information historique de chaque dème. Chaque cellule est représentée par un objet cell. Toutes les cellules sont agencées en une matrice, structure équivalente au grid dans un SIG. L'accès à chaque cellule se fait par un pointeur, ce qui facilite grandement leur accès, et permet de désallouer dynamiquement l'espace mémoire des cellules non-utilisées. L'objet cell contient un grand nombre de fonctions et de variables qui permettent de simuler la démographie et en particulier un objet State qui gère l'état environnemental et démographique courant (densité de population (N), capacité de soutien (K) et friction (F)).
La partie stockage de l'information en mémoire centrale (RAM) est assurée par une base de données, implémentée à travers un objet StateDB. Cet objet est un vecteur dont chaque 'case' est un pointeur vers un objet StatesOfCell, qui est lui-même lié à une cellule particulière par l'intermédiaire d'un pointeur et d'un index (nombre entier) unique. Cette double possibilité de connexion entre cell et StatesOfCell s'est avérée très utile pour optimiser certaines fonctions. Chaque objet StatesOfCell contient un minimum de cinq objets TimeSto qui vont stocker l'évolution, au cours du temps, des cinq variables qui sont la taille de population (1), le nombre d'émigrants 46 depuis le nord (2), depuis le sud (3), depuis l'est (4), et depuis l'ouest (5). L'objet TimeSto est discuté plus en détail dans les paragraphes qui suivent.

Les noms des classes des objets sont en italique. Voir le texte pour les explications.
Compression des données, l'objet TimeSto
La première solution a été dictée par la volonté de pouvoir compresser des séries de nombres identiques. Ces séries se rencontrent fréquemment dans la plupart des simulations, lorsque un dème n'est pas encore colonisé (série de zéros pour les migrations et la taille de population) ou lorsque la taille de population est stabilisée à la capacité de soutien. L'idée a été d'implémenter, dans l'objet TimeSto, un 'double vecteur', l'un contenant les valeurs de temps, et l'autre les données (Figure 6.9A). L'enregistrement d'une donnée (et du temps correspondant) se produit seulement si sa valeur diffère de celle de la donnée entrée auparavant.
La deuxième solution ne considère qu'un seul vecteur de données, mais l'index du vecteur sous lequel est trouvé une donnée correspond au temps (Figure 6.9B).

La structure en double vecteur est optimisée pour la compression, car aucune série de nombre identique n'est enregistrée. L'avantage de la structure en double vecteur diminue cependant avec l'augmentation des variations dans les séries de données. Lorsque les variations comptent pour la moitié des nombres entrés, les deux structures requièrent le même espace mémoire et si les variations sont encore plus fréquentes, la structure en simple vecteur est alors avantagée. Les cas produisant des variations peuvent être liés à l'environnement, si celui-ci est dynamique, ou peuvent découler d''effets de bord' (voir chapitre 0) qui produisent de petites variations autour de la capacité de soutien.
Pour ce qui est du temps d'exécution d'une simulation (démographique ou génétique), il est fortement conditionné par le temps d'accès aux données dans les objets TimeSto. La structure en simple vecteur est alors optimisée, car l'accès par l'index d'un vecteur y est alors bien plus rapide que la détermination, dans la structure en double vecteur, de la position de la donnée requise.
En fin de projet, les simulations en monde réaliste ont toutes été réalisées avec la structure TimeSto en simple vecteur. C'était alors la vitesse d'exécution d'une simulation (démographique, mais surtout génétique) que nous voulions diminuer, car plusieurs milliers de simulations devaient être lancées. Les contraintes sur la mémoire centrale étaient moins importantes et le monde réaliste utilisé (l'Ancien Monde en projection de Hammer) demandait environ 400 Mégabyte de mémoire.
Nous avons cependant voulu laisser la possibilité aux utilisateurs de FRICTION de pouvoir utiliser la structure en double vecteur. Celle-ci peut s'avérer indispensable si le nombre de dèmes considérés ou le nombre de générations devait être important. Pour s'en convaincre, il suffit de considérer la situation de l'Ancien Monde, simulé avec une résolution deux fois plus grande, ce qui signifie une largeur de dème deux fois plus petite. Dans ce cas, la mémoire requise serait d'environ 1,6 Gigabyte, excédant les capacités des ordinateurs à disposition.
6.4.3. Module génétique
L'implémentation de la coalescence dans FRICTION est basée sur un certain nombre d'objets. Les objets principaux, ainsi que les relations qui les lient, sont schématisés dans la Figure 6.10. La base de données génétiques est un membre de World et est représentée par l'objet TDemeCollection. Cet objet contient premièrement un vecteur de dèmes (objets TDemes). Chaque dème est lié de manière unique à une cellule par un pointeur et un index. Ce lien permet au dème d'accéder à l'historique démographique de la cellule, cet historique étant indispensable pour le processus de coalescence. L'objet TDemeCollection contient également un objet Tree, qui permet de stocker la topologie de l'arbre de coalescence. Au cours du processus de coalescence, cet arbre est mis à jour via un objet TNodeList, qui est une liste dynamique permettant de maintenir des pointeurs vers les noeuds courants de l'arbre.
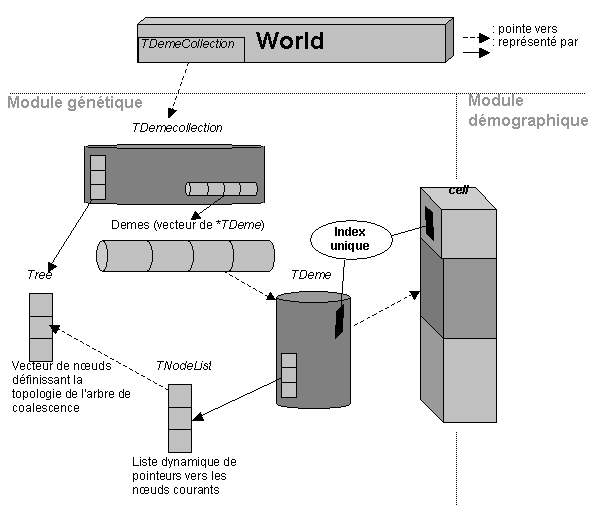
Les noms des classes des objets sont en italique. Voir le texte pour les explications.
6.4.4. Modèles démographiques disponibles
Six modèles démographiques de dits 'de base' sont implémentés dans FRICTION, et portent chacun un identificateur numérique (1-6). Le Tableau 6.5. résume ces modèles qui ont été discutés en détail dans le chapitre 4.2.3. (pour le modèle linéaire simple et le modèle densité-dépendant) et à l'0 pour le modèle de diffusion classique.
Nous avons également rendu la structure de FRICTION suffisamment souple pour pouvoir facilement étendre les modèles de base ou créer d'autres modèles. Chaque nouveau modèle développé doit alors recevoir un identificateur unique qui sera appelé par la fonction World::IterateCells(). Comme l'identificateur du modèle voulu est un paramètre du fichier de configuration (fichier Settings, voir 0), il est aisé de créer plusieurs de ces fichiers lorsque l'on désire procéder à un jeux de simulation en utilisant plusieurs modèles démographiques alternatifs.
Le modèle 1 ne peut être utilisé pour la coalescence car il n'y a pas de flux migratoire à l'équilibre.
6.4.5. Exemple de fichier Settings
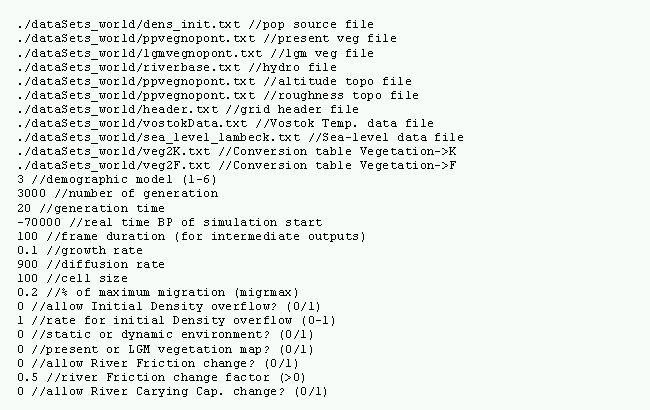
Le fichier Settings est le fichier comprenant les valeurs de tous les paramètres environnementaux, démographiques et génétiques utilisés lors d'une simulation dans le programme FRICTION. L'exemple ci-dessous donne des exemples de valeurs pour les 58 paramètres actuellement implémentés. Ce qui suit les doubles slash (//) est une description du paramètre se trouvant sur la même ligne.

6.4.6. Arrondis des nombres
Les contraintes dues à la coalescence nous ont obligé à ne travailler qu'avec des nombres entiers d'individus (pour les densités de populations et les nombres de migrants). Plusieurs solutions ont été testées pour l'arrondi.
Nous avons retenu la méthode qui a consisté à stocker la partie fractionnaire d'un nombre réel d'une génération à l'autre. Seule la partie entière est traitée dans la génération présente. A la génération suivante, la nouvelle partie fractionnaire est ajoutée à la partie fractionnaire obtenue lors de la génération précédente. Lorsque la somme s des éléments fractionnaires dépasse l'unité, un individu est ajouté et s prend comme nouvelle valeur s-1.
Cette méthode a l'avantage de ne pas demander de tirage de nombres aléatoires pour l'arrondi. Elle est, de ce fait, optimisée pour une application où le temps d'exécution d'une simulation doit être minimisé. Notons que cette méthode va toujours donner un nombre entier d'individus égal ou inférieur à la valeur réelle. La somme des individus au cours de la croissance va donc être légèrement sous-estimée, ce que nous avons décidé de négliger dans notre étude.
6.5. Diffusion classique
Cette Annexe discute du modèle de la diffusion classique dit de Fisher-Skellam (Fisher (1937) et Skellam (1951)). Cette discussion est centrée principalement sur la manière de discrétiser l'équation différentielle qui est à la base du modèle (voir Hazelwood et Steele, 2003).
La dispersion d'individus est représentée sous la forme d'une équation différentielle composée d'un terme de croissance de population et d'un terme de dispersion (ou diffusion). Le terme de croissance correspond à la croissance logistique qui a été discutée de manière détaillée au chapitre 0 Le changement de la population au cours du temps et le long d'un espace unidimensionnel et continu est décrit par l'équation
 |
(6.6) |
où  est la densité de population,
est la densité de population,  le temps,
le temps,  la localisation géographique,
la localisation géographique,  le taux de croissance,
le taux de croissance,  la capacité de soutien, et
la capacité de soutien, et 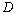 la constante de diffusion (unité de distance2/unité de temps).
la constante de diffusion (unité de distance2/unité de temps).
Pour implémenter la diffusion dans un espace discret, cette équation doit être discrétisée temporellement et spatialement, tout en conservant ses propriétés associées avec l'équation continue sous-jacente. Commençons par considérer la partie temporelle de l'équation. Nous devons nous assurer que les changements de densité de population soient petits par rapport au temps. Si nous considérons les deux termes séparément, le changement de population dû à la croissance est donné par la partie logistique 
Pour comprendre comment se comporte la croissance initiale de la population, nous pouvons prendre la composante linéaire de l'équation précédente 
Nous nous intéressons à l'échelle de temps 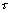 pour laquelle survient un changement de densité de population. Pour un petit changement de densité, nous pouvons laisser tomber les dérivées partielles comme suit
pour laquelle survient un changement de densité de population. Pour un petit changement de densité, nous pouvons laisser tomber les dérivées partielles comme suit 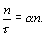
Divisant par n et réarrangeant, l'échelle de temps au cours de laquelle la population change est donnée par
 |
(6.7) |
Pour une application numérique, il faut donc s'assurer que le pas de temps est plus petit que  pour conserver d'une part la propriété de continuité de la croissance de population, et d'autre part la stabilité numérique. Cette dernière n'est néanmoins pas l'intérêt principal ici, et il existe des analyses plus détaillées que déterminent les conditions exactes de stabilité (par ex. Press et al., 1992, Chap. 1.4; Iserles, 1996).
pour conserver d'une part la propriété de continuité de la croissance de population, et d'autre part la stabilité numérique. Cette dernière n'est néanmoins pas l'intérêt principal ici, et il existe des analyses plus détaillées que déterminent les conditions exactes de stabilité (par ex. Press et al., 1992, Chap. 1.4; Iserles, 1996).
Le terme de diffusion peut être considéré de manière similaire. Un petit changement de densité peut être décrit par 
Le temps pour que la population disperse d'une distance 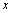 de la source est donc approximé par
de la source est donc approximé par
 |
(6.8) |
De manière similaire à l'équation (6.7), pour conserver la nature continue du processus de diffusion, nous devons nous assurer que la population ait assez de temps pour disperser dans les cellules voisines. Il faut donc s'assurer que le pas de temps est plus petit que 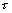 .
.
Les deux restrictions données par les équations (6.7) et (6.8) s'appliquent uniquement aux changements continus de la population avec le temps. Il y a également une restriction du changement de la population dans l'espace. Nous devons nous assurer que les changements se produisent assez lentement à l'échelle spatiale de notre grille de cellules. Cette information peut être obtenue en comparant les termes de croissance et de diffusion utilisés plus haut, comme suit 
En réarrangeant pour  , nous obtenons la distance pour laquelle ce processus change naturellement (réécrit
, nous obtenons la distance pour laquelle ce processus change naturellement (réécrit 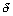 )
)
 |
(6.9) |
Pour maintenir la résolution de la vague de progression de la population, nous devons donc maintenir la taille de nos cellules inférieure à  .
.
En résumé, pour s'assurer que nous modélisons l'équation continue et non son homologue discret, les conditions sur le temps et l'espace sont  ,
, 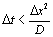 et
et 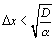 . Des valeurs utilisées avec succès sont un facteur de 5 pas de temps par
. Des valeurs utilisées avec succès sont un facteur de 5 pas de temps par  , et 10 cellules par
, et 10 cellules par 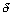 (Lee Hazelwood, comm. pers.).
(Lee Hazelwood, comm. pers.).
Les différentiels de surface discrétisés sont approximés par (Steele et al., 1995) 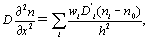 où
où  et
et  sont respectivement les indices de la cellule focale et d'une cellule voisine,
sont respectivement les indices de la cellule focale et d'une cellule voisine,  la longueur de la cellule,
la longueur de la cellule,  le coefficient de pondération de la somme dans le cas de 8 voisins (suivant que l'on se trouve le long des axes (2/3) ou le long des diagonales (1/6)), et
le coefficient de pondération de la somme dans le cas de 8 voisins (suivant que l'on se trouve le long des axes (2/3) ou le long des diagonales (1/6)), et 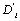 le paramètre de diffusion effectif, qui détermine la mobilité entre deux cellules. Ce dernier paramètre est donné par
le paramètre de diffusion effectif, qui détermine la mobilité entre deux cellules. Ce dernier paramètre est donné par
 |
(6.10) |
où  et
et 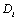 sont respectivement les constantes de diffusion de la cellule focale et d'une cellule voisine. La constante de diffusion
sont respectivement les constantes de diffusion de la cellule focale et d'une cellule voisine. La constante de diffusion  représente le degré de mobilité d'un individu. En général, les individus peuvent se mouvoir depuis leur lieu de naissance d'une distance
représente le degré de mobilité d'un individu. En général, les individus peuvent se mouvoir depuis leur lieu de naissance d'une distance 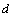 pendant le temps de génération
pendant le temps de génération  . Le carré de cette distance sera normalement proportionnel au temps disponible. La constante de proportionnalité est la constante de diffusion
. Le carré de cette distance sera normalement proportionnel au temps disponible. La constante de proportionnalité est la constante de diffusion 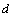 , et s'exprime par
, et s'exprime par 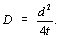
Mentionnons finalement que les résultats analytiques sur la vitesse de la vague de progression en deux dimensions donne une vitesse égale à  (van den Bosch et al., 1992). Il y a donc une importance similaire du taux de croissance et de la constante de diffusion pour cette vitesse d'expansion, et donc pour le temps de colonisation d'une surface donnée.
(van den Bosch et al., 1992). Il y a donc une importance similaire du taux de croissance et de la constante de diffusion pour cette vitesse d'expansion, et donc pour le temps de colonisation d'une surface donnée.
6.6. Visualisation des variations démographiques
Pour visualiser les changements de migrations dus aux processus de colonisation ou à la variation des capacités de soutien et des frictions, nous avons implémenté un mécanisme s'inspirant des représentations météorologiques des directions et forces des vents. Un facteur d'agrégation 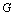 des cellules est premièrement défini. Il groupe
des cellules est premièrement défini. Il groupe  cellules, où
cellules, où  est un ensemble carré (1, 4, 9, 16, etc.), de sorte que
est un ensemble carré (1, 4, 9, 16, etc.), de sorte que 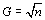 . Le nombre directionnel de migrants est alors déterminé par
. Le nombre directionnel de migrants est alors déterminé par
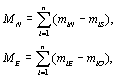 |
(6.11) |
où 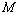 indique le nombre de migrants directionnel moyen,
indique le nombre de migrants directionnel moyen,  indique le nombre de migrants directionnel locaux, et les indices
indique le nombre de migrants directionnel locaux, et les indices 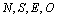 indiquent respectivement le nord, le sud, l'est et l'ouest. La direction principale d'où provient l'immigration 47 est alors représentée comme une moyenne des vecteurs
indiquent respectivement le nord, le sud, l'est et l'ouest. La direction principale d'où provient l'immigration 47 est alors représentée comme une moyenne des vecteurs 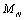 et
et  .
.
|
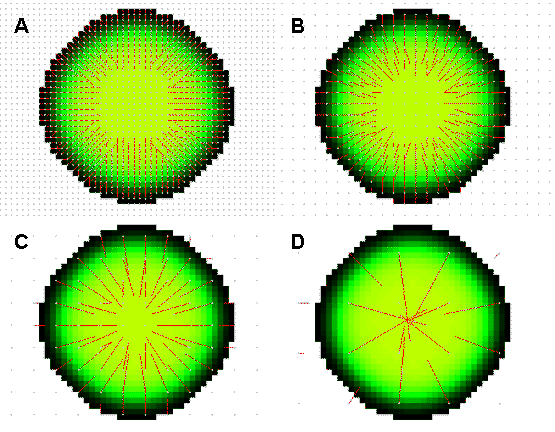
(A) G=1, (B) G=2, (C) G=4, (D) G=9 |
Les points définissent le centre d'un agrégat de cellules, et les traits la direction de l'immigration vers le centre de l'agrégat. La longueur d'un trait est proportionnelle au nombre d'immigrants.
La Figure 6.11. donne des exemples de visualisation graphique en faisant varier la valeur d'agrégation. On remarque qu'une valeur d'agrégation de 1 (Figure 6.11. :A, une seule cellule prise en considération) ne donne que la direction préférentielle de migration, sans la valeur relative du nombre de migrants (les longueurs des barres sont toutes égales à 1), ceci afin de garder une certaine lisibilité de la carte. Une forte valeur d'agrégation donne peu d'information (Figure 6.11. :D) puisque les résultats représentent alors un résumé sur un grand nombre de cellules, en gommant les fluctuations locales qui sont justement intéressantes lorsque l'environnement est hétérogène. On préférera en générale une valeur d'agrégation de 2 à 4 pour une visibilité optimale (Figure 6.11. :B,C).
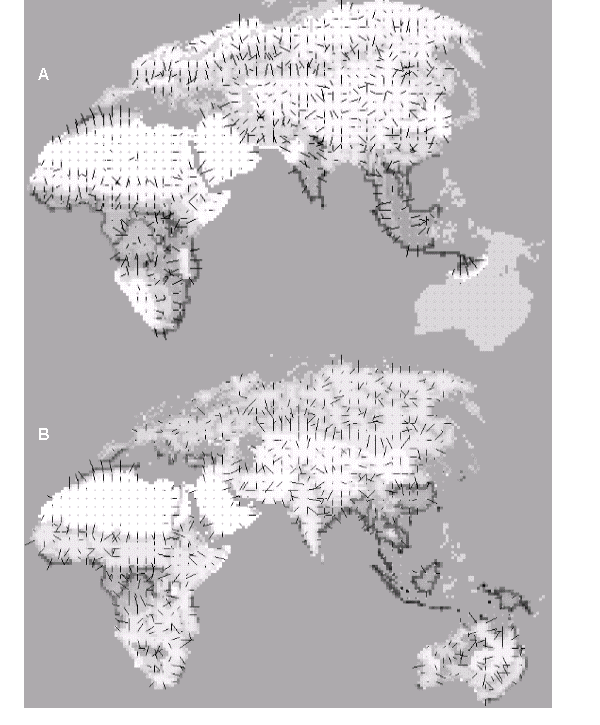
L'utilisation de cette méthode dans un monde réaliste et subissant un dynamisme environnemental est encore plus intéressante. En effet, elle permet d'étudier des variations démographiques comme des changements de directions ou d'intensités de l'immigration. La Figure 6.12 montre les directions de migration pour deux états temporels d'une simulation d'expansion mondiale en milieu dynamique. Nous pouvons par exemple remarquer une immigration vers le centre du Sunda (plateau émergé du sud-est asiatique) dans la Figure 6.12A, dues aux densités de populations plus fortes sur les côtes induisant des migrations vers le centre du territoire, ou encore les migrations relativement homogènes du centre de l'Europe dans la Figure 6.12B, dues à un environnement peu hétérogène pendant cette période.
|
(A) -25 ka, |
Le facteur d'agrégation est de trois.
6.7. Analyses de sensibilité - aspects techniques
Nous commençons par discuter, dans cette Annexe, des différents types d'analyse de sensibilité disponibles. Nous poursuivons par expliquer de manière détaillée les analyses de sensibilité basées sur la variance qui ont été utilisées aux chapitres 0 et 0. Nous finissons par donner les résultats tabulaires obtenus dans ces mêmes deux chapitres.
6.7.1. Les différents types d'analyse de sensibilité
Avant de définir les grandes classes d'AS et de voir plus en détail les méthodes employées dans ce travail, il nous a semblé important de discuter brièvement de ce qui se fait généralement en lieu et place d'une AS classique. Nous allons décrire trois techniques fréquemment utilisées (car faciles d'emploi), mais qui présentent néanmoins des limites, essentiellement en rapport avec la complexité du modèle étudié.
Techniques fréquemment utilisées
Du fait de sa grande simplicité, l'une des approches les plus souvent employées consiste à procéder à une analyse de perturbation (Rahni, 1998): le modèle est simulé pour une valeur de base d'un paramètre, puis pour une ou plusieurs valeurs perturbées de ce même paramètre, les autres paramètres étant maintenus constants. Le comportement des résultats est alors comparé avec la simulation de base, moyennant des hypothèses de linéarité et d'indépendance des paramètres. Cette méthode permet de dire si le modèle est 'très' ou 'peu' sensible aux variations d'un paramètre et de regarder dans quelle direction dévie la sortie du modèle, mais elle est vite limitée lorsque les modèles font intervenir des grands jeux de paramètres, ou présentent d'importants effets non linéaires. De plus, il est rare que la totalité des paramètres soit passée en revue, et les paramètres jugés a priori influents (donc ceux qui sont perturbés) ne sont pas choisis suivant une procédure systématique, mais une procédure qui relève d'un jugement arbitraire.
L'analyse de perturbation peut également être utilisée avec des modèles pour lesquels il n'est pas possible de sortir une statistique numérique d'un résultat. Cela a été le cas, par exemple, pour notre étude de la diversité moléculaire, présentée dans le chapitre 4.4. Dans cette étude, nous avions travaillé, entre autres, avec la distribution mismatch des différences par paire de gènes. Différentes valeurs étaient choisies pour certains paramètres (comme la capacité de soutien ou le taux de migration), et les distributions mismatchs obtenues étaient comparées graphiquement.
Pour ce qui est de la quantification de l'incertitude d'un résultat compte tenu des imprécisions des paramètres, la méthode de Monte Carlo a largement fait ses preuves dans des domaines très diversifiés (Brooks, 1998). Une fois fixée la distribution de probabilité de paramètres d'entrée, ces paramètres sont échantillonnés de façon aléatoire dans leur plage de variation et suivant la distribution qui les caractérise. Pour chaque combinaison (également aléatoire) de ces valeurs échantillonnées, la sortie du modèle est calculée. La théorie probabiliste garantit que le spectre des sorties ainsi obtenu fournit une bonne représentation de la distribution réelle des résultats, et il est alors possible d'obtenir l'estimation non-biaisée de grandeurs statistiques (par ex. moyenne, écart-type, intervalle de confiance). Bien que cette méthode ait l'avantage d'une mise en oeuvre facile, elle nécessite, pour une bonne précision des résultats, un nombre de simulations très élevé: elle est donc difficile à utiliser lorsque le modèle est onéreux en temps de calcul et que les paramètres sont nombreux.
Enfin, et en ce qui concerne l'amélioration des résultats d'un modèle, le calage 'manuel' du modèle en agissant sur quelques paramètres représente la procédure la plus largement appliquée. Cette méthode tend à faire coïncider le modèle avec des données externes sans une réelle procédure de validation. Elle indique alors, tout au plus, une combinaison de paramètres qui apporte une réduction du résidu (variance non expliquée), mais qui ne permet pas l'identification d'une solution optimale. Elle n'est de plus envisageable que sur un jeu de paramètres très restreint.
Ces techniques sont appropriées pour des configurations de modèles simples, ou pour des modèles pour lesquels il n'est pas possible d'automatiser la réponse étudiée. La plupart du temps, il est cependant possible d'utiliser des techniques d'AS ayant une approche statistique robuste, ce dont nous allons parler maintenant.
Les grandes classes d'AS
Les différentes techniques d'AS peuvent être classées de plusieurs manières. Si certains auteurs utilisent une classification méthodologique (par exemple méthodes mathématiques, statistiques et graphiques (Frey et Patil, 2002)), d'autres préfèrent une classification basée sur les capacités des différentes techniques (screening, locales et globales (Saltelli, 2000)). Nous utiliserons cette dernière classification puisqu'elle permet de mieux cerner les besoins pour le présent travail.
Lorsqu'un modèle a un temps d'exécution très long et qu'il comporte de très nombreux paramètres (typiquement >100), les méthodes de screening permettent d'identifier la (généralement) petite partie des paramètres qui contrôle la plupart de la variabilité des résultats. Ces méthodes ont l'avantage de ne demander qu'un petit nombre d'évaluations du modèle, et sont généralement basées sur une configuration un-à-la-fois (one-at-a-time, OAT) dans laquelle l'impact du changement d'un paramètre est évalué alors que les autres paramètres restent constants. Une valeur 'standard' est choisie pour chaque paramètre, se situant généralement au milieu de deux valeurs dites 'extrêmes'. Les magnitudes des résidus, définies comme les différences entre les résultats de l'expérience perturbée et du contrôle, sont alors comparées afin de déterminer les paramètres responsables de la plus grande variation des résultats du modèle. Une limitation des OAT est qu'elles ne permettent l'évaluation que des effets de premier ordre (ou effets principaux, c'est-à-dire les effets des paramètres d'entrée en excluant leurs interactions mutuelles). De plus, elles ne permettent qu'une classification par ordre d'importance des paramètres, sans pouvoir quantifier cette importance en donnant un pourcentage de la variance des résultats due à chaque paramètre.
Parmi les différentes méthodes de screening existantes (voir une revue dans Campolongo et al., 2000a), la méthode de Morris (Morris, 1991) est particulièrement recommandée pour les cas où le nombre d'évaluations du modèle doit être proportionnel au nombre de paramètres. Cette méthode possède également l'avantage de ne pas demander d'hypothèses simplificatrices sur la structure du modèle, comme la plupart des autres méthodes de screening. Elle permet de plus de déterminer les effets principaux et totaux, mais ne permet pas l'analyse d'incertitude. Un exemple d'une application de la méthode de Morris en écologie portant sur la dynamique des populations de la sardine peut être trouvé dans Zaldívar Comenges et Campolongo (2000). La méthode de Morris se base sur l'évaluation de l'effet élémentaire (elementary effect, (Morris, 1991)) d'un paramètre 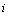 à un point donné
à un point donné 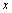 de l'espace
de l'espace 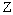 des paramètres d'entrée comme étant
des paramètres d'entrée comme étant
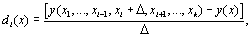 |
(6.12) |
où 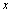 est n'importe quel point dans
est n'importe quel point dans  tel que
tel que  est encore dans
est encore dans 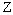 (
( est une petite valeur de perturbation). Une distribution
est une petite valeur de perturbation). Une distribution  des effets élémentaires du paramètre
des effets élémentaires du paramètre  est alors obtenue en échantillonnant
est alors obtenue en échantillonnant 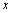 à partir de
à partir de 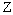 . L'information sur l'influence du paramètre
. L'information sur l'influence du paramètre 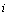 sur la réponse du modèle est alors obtenue à travers la moyenne
sur la réponse du modèle est alors obtenue à travers la moyenne  et l'écart-type
et l'écart-type 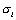 de la distribution
de la distribution 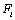 . Une grande moyenne indique une grande influence du paramètre sur la sortie, alors qu'un grand écart-type indique que le paramètre interagit avec d'autres paramètres ou que son effet est non linéaire. Un exemple de résultats d'une analyse de Morris est donné dans la Figure 6.13.
. Une grande moyenne indique une grande influence du paramètre sur la sortie, alors qu'un grand écart-type indique que le paramètre interagit avec d'autres paramètres ou que son effet est non linéaire. Un exemple de résultats d'une analyse de Morris est donné dans la Figure 6.13.
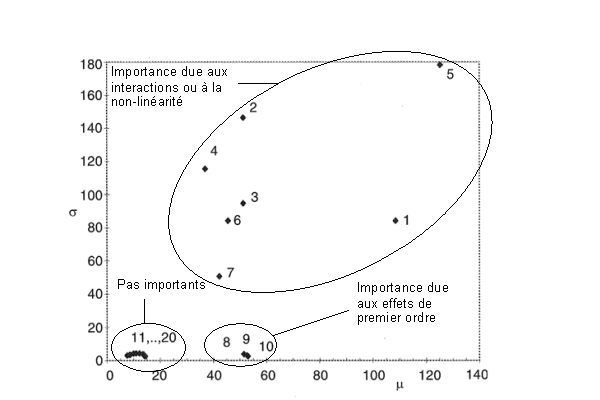
L'importance des groupes de paramètre est indiquée. Les axes correspondent à la moyenne et à l'écart-type de la distribution des effets élémentaires.
Le nombre requis d'évaluations du modèle pour une analyse de Morris est égal à 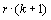 , où
, où 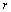 est le nombre d'effets élémentaires calculé par paramètre. Ce dernier nombre varie selon les applications, mais on lui donne souvent une valeur relativement basse (par ex. 10, dans Zaldívar Comenges et Campolongo, 2000).
est le nombre d'effets élémentaires calculé par paramètre. Ce dernier nombre varie selon les applications, mais on lui donne souvent une valeur relativement basse (par ex. 10, dans Zaldívar Comenges et Campolongo, 2000).
Les méthodes locales (ou méthodes d'analyses différentielles) se concentrent sur l'impact local des paramètres sur le modèle. Ces méthodes sont généralement basées sur le calcul de dérivées partielles de la fonction de sortie du modèle en utilisant les paramètres d'entrée. De façon à déterminer les dérivées de manière numérique, les paramètres d'entrée varient dans un intervalle relativement petit autour d'une valeur nominale. L'intervalle est généralement le même pour tous les paramètres (par ex. 10% de la valeur nominale). Une mesure typique de sensibilité locale  est donnée par
est donnée par  c'est-à-dire l'effet sur la variation relative de la sortie
c'est-à-dire l'effet sur la variation relative de la sortie  de perturber un paramètre
de perturber un paramètre 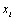 par une fraction fixée de la valeur nominale de
par une fraction fixée de la valeur nominale de  .
.  peut être estimé par
peut être estimé par 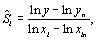 où l'indice
où l'indice  indique une valeur nominale du paramètre et de sa sortie.
indique une valeur nominale du paramètre et de sa sortie.
Contrairement aux méthodes globales que nous allons voir par la suite, il n'est donc pas possible avec les méthodes locales de déterminer l'impact de possibles différences dans l'échelle de variation des paramètres d'entrée du modèle (ces échelles de variation étant par exemple reliées à l'incertitude sur chaque paramètre). De nombreuses méthodes d'AS locales ont été développées. Elles reposent souvent sur de complexes analyses différentielles, et sur leurs techniques d'approximation comme les séries de Taylor. Une revue poussée de la théorie et des méthodes peut être trouvée dans Turányi et Rabitz (2000). Les méthodes locales sont principalement utilisées lorsque le modèle est connu comme étant linéaire, comme c'est typiquement le cas pour certaines réactions cinétiques en chimie. Il a été démontré depuis longtemps ((Cukier et al., 1973), cité dans (Saltelli, 2000)) qu'une méthode globale devrait être utilisée lorsque le modèle est non linéaire et que plusieurs paramètres sont affectés par des incertitudes.
Les méthodes globales tendent à attribuer quantitativement l'incertitude de la sortie d'un modèle aux incertitudes des paramètres d'entrée, qui sont typiquement décrites par des fonctions de distribution de probabilité qui couvrent l'intervalle des valeurs possibles attribuées à chaque paramètre. Le choix de ces intervalles est important puisqu'il représente le degré de connaissance du modèle et de sa paramétrisation. De manière plus spécifique, les méthodes globales peuvent être définies à l'aide de deux de leurs propriétés:
- l'inclusion de l'influence de l'intervalle et de la forme: les estimations de sensibilité de chaque paramètre incorporent l'effet de la grandeur de l'intervalle et de la forme de la fonction de distribution de probabilité;
- la moyenne multidimensionnelle (multidimensional averaging): les estimations de sensibilité de chaque paramètre sont évaluées alors que tous les autres paramètres varient en même temps (contrairement aux méthodes de screening et aux méthodes locales).
Les méthodes globales utilisent pour la plupart les analyses dites de Monte Carlo. Ces dernières sont basées sur des évaluations multiples d'un modèle en utilisant des valeurs de paramètres d'entrée sélectionnées aléatoirement, puis en utilisant les résultats de ces évaluations pour quantifier l'incertitude des prédictions du modèle et l'apport de chaque paramètre à cette incertitude. L'utilisation de ces méthodes globales implique généralement cinq étapes distinctes qui sont:
- la sélection de l'intervalle de valeur des paramètres et de leur distribution;
- la génération d'un échantillon à partir des intervalles et distributions du point 1;
- l'évaluation du modèle pour chaque élément de l'échantillon;
- l'analyse d'incertitude;
- l'analyse de sensibilité.
Lors de l'étape 1, le modélisateur est souvent confronté à l'absence d'information sur l'intervalle et la distribution des paramètres. En effet, même si certains paramètres ont pu être estimés par des données de terrain ou par des méthodes statistiques, ils sont souvent inadéquats puisqu'ils ont été estimés à une échelle de temps, ou une échelle physique, bien plus petite que l'échelle nécessaire pour le modèle. De plus, certains paramètres du modèle peuvent ne pas être observables, alors que d'autres peuvent représenter l'apparition d'un phénomène rare (par ex. un événement climatique majeur comme une glaciation). En l'absence d'information exhaustive sur les paramètres, il convient de faire l'hypothèse de distributions uniformes (ou log uniformes), et de s'en remettre au réalisme physique des valeurs des intervalles. Notons que les résultats d'analyses de sensibilité dépendent souvent davantage des intervalles de valeur donnés aux paramètres que de leurs distributions (Campolongo et al., 2000b).
L'étape 2, l'échantillonnage des valeurs d'entrée, peut utiliser des procédures diverses, dont les plus courantes sont l'échantillonnage aléatoire, l'échantillonnage stratifié (par ex. échantillonnage Hypercube Latin, permettant une meilleure couverture de l'espace des valeurs en partitionnant cet espace en sous-espaces échantillonnés aléatoirement), et l'échantillonnage quasi-aléatoire (basé sur des séquences pouvant améliorer la convergence des résultats sous certaines conditions).
L'étape 3 est l'évaluation du modèle, conceptuellement simple puisqu'il s'agit de fournir au modèle chaque élément de l'échantillonnage composé des valeurs des 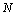 paramètres. Une séquence de résultats de la forme
paramètres. Une séquence de résultats de la forme  est alors créée et sera utilisée dans les deux dernières étapes.
est alors créée et sera utilisée dans les deux dernières étapes.
L'étape 4, l'analyse d'incertitude, est triviale. Il s'agit d'examiner la ou les distributions des variables de sortie du modèle. Une inspection visuelle de cette distribution et des valeurs extrêmes peut mener dans certains cas à une restructuration du modèle. En effet, si la distribution d'une sortie 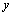 n'est pas satisfaisante (par exemple des valeurs trop élevées dans une analyse de risque environnemental), il n'y a pas de raison de procéder à la cinquième étape. L'analyse d'incertitude permet également d'estimer l'espérance et la variance de la variable réponse
n'est pas satisfaisante (par exemple des valeurs trop élevées dans une analyse de risque environnemental), il n'y a pas de raison de procéder à la cinquième étape. L'analyse d'incertitude permet également d'estimer l'espérance et la variance de la variable réponse 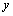 par
par
 |
(6.13) |
 |
(6.14) |
La dernière étape est l'analyse de sensibilité, permettant d'attribuer quantitativement la variation des résultats aux différentes sources de variation du système. De nombreuses méthodes existent, aboutissant à des mesures de sensibilité distinctes. Nous allons commenter quelques-unes de ces méthodes, en terminant sur les cas particuliers des analyses de Monte Carlo basées sur la variance.
Parmi les méthodes d'analyses de sensibilité simples et intuitives, nous retrouvons l'analyse graphique par nuage de points (scatterplot). Il s'agit de représenter graphiquement chaque réponse 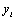 contre chaque valeur
contre chaque valeur  de chaque paramètre
de chaque paramètre 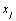 , où
, où  , et
, et  . Ces graphiques peuvent révéler des relations non linéaires entre les paramètres d'entrée et les réponses du modèle. Le désavantage majeur de ces méthodes est qu'elles nécessitent la génération et l'examen d'au moins un graphique par paramètre, potentiellement multiplié par le nombre de pas de temps si la réponse du modèle est dépendante du temps. De plus, les méthodes en nuage de points n'offrent qu'une mesure qualitative de la sensibilité puisque l'importance relative de chaque paramètre peut être estimée, mais non quantifiée.
. Ces graphiques peuvent révéler des relations non linéaires entre les paramètres d'entrée et les réponses du modèle. Le désavantage majeur de ces méthodes est qu'elles nécessitent la génération et l'examen d'au moins un graphique par paramètre, potentiellement multiplié par le nombre de pas de temps si la réponse du modèle est dépendante du temps. De plus, les méthodes en nuage de points n'offrent qu'une mesure qualitative de la sensibilité puisque l'importance relative de chaque paramètre peut être estimée, mais non quantifiée.
Une autre mesure simple de la sensibilité est donnée par le très répandu coefficient de corrélation linéaire de Pearson (voir par ex. Sokal et Rohlf, 1981, p. 565), calculé sur les points 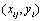 . Le coefficient de corrélation
. Le coefficient de corrélation 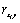 entre le paramètre d'entrée
entre le paramètre d'entrée 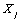 et la sortie
et la sortie 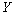 représente une mesure de leur relation linéaire. En utilisant le rang de
représente une mesure de leur relation linéaire. En utilisant le rang de  et de
et de  en lieu et place de leur valeur brute, on obtient le coefficient de corrélation de Spearman, préféré en présence d'un modèle non linéaire.
en lieu et place de leur valeur brute, on obtient le coefficient de corrélation de Spearman, préféré en présence d'un modèle non linéaire.
Des méthodes de sensibilité sont basées sur l'analyse de régression menant à la détermination de coefficients de régression standardisés (standardized regression coefficients, SRCs). Ces coefficients peuvent être utilisés pour l'analyse de sensibilité (si les paramètres sont indépendants) puisque qu'ils quantifient l'effet de la variation de chaque paramètre éloigné de sa moyenne par une fraction fixée de sa variance. Lors de l'utilisation des SRCs, il est important de considérer le coefficient de détermination  qui donne une mesure de la capacité du modèle de régression linéaire à reproduire la réponse
qui donne une mesure de la capacité du modèle de régression linéaire à reproduire la réponse 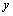 . Ce coefficient représente la fraction de la variance des résultats expliquée par le modèle de régression, et la performance du modèle augmente avec
. Ce coefficient représente la fraction de la variance des résultats expliquée par le modèle de régression, et la performance du modèle augmente avec  s'approchant de l'unité. Lorsque la relation entre paramètre d'entrée et réponse du modèle est non linéaire, une transformation des données en leurs rangs respectifs est possible. Une analyse de régression typique est alors utilisée sur ces données transformées, et l'on obtient un coefficient de détermination basé sur les rangs
s'approchant de l'unité. Lorsque la relation entre paramètre d'entrée et réponse du modèle est non linéaire, une transformation des données en leurs rangs respectifs est possible. Une analyse de régression typique est alors utilisée sur ces données transformées, et l'on obtient un coefficient de détermination basé sur les rangs 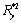 . Si
. Si  est plus grand que
est plus grand que  , les coefficients de régression standardisés en rang (standardized rank regression coefficients, SRRCs) peuvent être utilisés. Notons qu'une différence entre
, les coefficients de régression standardisés en rang (standardized rank regression coefficients, SRRCs) peuvent être utilisés. Notons qu'une différence entre  et
et 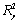 est un indicateur utile de la non linéarité d'un modèle.
est un indicateur utile de la non linéarité d'un modèle.
Les performances des SRRCs sont très satisfaisantes lorsque les réponses d'un modèle varient de manière monotone avec chaque paramètre indépendant. Avec la présence d'un modèle fortement non monotone, les résultats de l'analyse peuvent néanmoins devenir très mauvais ( bas). Une autre limitation à l'utilisation de ces statistiques par rang est qu'elles altèrent le modèle étudié, de sorte que les indices de sensibilité générés renseignent sur un modèle différent. Ce nouveau modèle est non seulement plus linéaire que le modèle original, mais il est également plus additif 48 . Il en résulte que l'importance des paramètres qui agissent sur les résultats par le biais d'interactions peut être sous-estimée.
bas). Une autre limitation à l'utilisation de ces statistiques par rang est qu'elles altèrent le modèle étudié, de sorte que les indices de sensibilité générés renseignent sur un modèle différent. Ce nouveau modèle est non seulement plus linéaire que le modèle original, mais il est également plus additif 48 . Il en résulte que l'importance des paramètres qui agissent sur les résultats par le biais d'interactions peut être sous-estimée.
Des tests statistiques basés sur deux échantillons (two-sample test statistics), comme le t-test, ont également été employés comme mesure de sensibilité. L'idée est ici de partitionner l'échantillonnage des valeurs d'entrée d'un paramètre 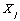 en deux sous-échantillons déterminés par les quantiles de la distribution de la sortie
en deux sous-échantillons déterminés par les quantiles de la distribution de la sortie  . Si les distributions de
. Si les distributions de  dans les deux sous-échantillons sont statistiquement dissemblables, le paramètre
dans les deux sous-échantillons sont statistiquement dissemblables, le paramètre  est alors considéré comme influençant la sortie
est alors considéré comme influençant la sortie 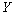 . Bien qu'intéressante, l'application de ces tests pour l'analyse de sensibilité souffre de plusieurs défauts. Les estimations dérivées de ces tests ne sont pas très robustes ((Saltelli et Marivoet, 1990), cité dans (Campolongo et al., 2000b)), et elles tendent à être qualitatives. De plus, les résultats dépendent fortement du choix des quantiles pour la séparation des sous-échantillons. Ces méthodes ne sont donc pas recommandées, à moins d'une application particulière dans laquelle une portion fixée de la queue d'une distribution d'une variable de sortie d'un modèle doive nécessairement être caractérisée.
. Bien qu'intéressante, l'application de ces tests pour l'analyse de sensibilité souffre de plusieurs défauts. Les estimations dérivées de ces tests ne sont pas très robustes ((Saltelli et Marivoet, 1990), cité dans (Campolongo et al., 2000b)), et elles tendent à être qualitatives. De plus, les résultats dépendent fortement du choix des quantiles pour la séparation des sous-échantillons. Ces méthodes ne sont donc pas recommandées, à moins d'une application particulière dans laquelle une portion fixée de la queue d'une distribution d'une variable de sortie d'un modèle doive nécessairement être caractérisée.
Il existe d'autres méthodes complexes basées sur les simulations de Monte Carlo (pour une description détaillée, voir par exemple Helton et Davis, 2002a; 2002b) en plus de celles décrites dans les paragraphes précédents. Ces autres méthodes sont généralement appliquées dans des cas particuliers qu'il n'est pas nécessaire de développer ici. Les derniers types d'analyses de sensibilité globales que nous allons étudier plus en détail sont les analyses basées sur la variance.
6.7.2 Méthodes d'analyse de sensibilité basées sur la variance
Les méthodes basées sur la variance sont des méthodes d'analyses de sensibilité globales qui peuvent être utilisées en conjonction avec des simulations de Monte Carlo, et qui sont basées sur l'estimation de la fraction de la variance de 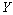 expliquée par le paramètre
expliquée par le paramètre 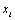 :
:
 |
(6.15) |
où 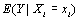 représente l'espérance de
représente l'espérance de  conditionnée par une valeur fixée de
conditionnée par une valeur fixée de  , et
, et  indique la variance sur toutes les valeurs possible de
indique la variance sur toutes les valeurs possible de  .
.  est communément appelé la mesure d'importance (measure of importance) ou encore la ration de corrélation (correlation ratio). Elle est calculée comme étant la variance, pour toutes les valeurs possibles de
est communément appelé la mesure d'importance (measure of importance) ou encore la ration de corrélation (correlation ratio). Elle est calculée comme étant la variance, pour toutes les valeurs possibles de 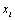 , de l'espérance conditionnelle de
, de l'espérance conditionnelle de 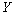 , normalisée par la variance totale de
, normalisée par la variance totale de 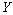 . Les différentes méthodes d'évaluation de la mesure d'importance qui existent se concentrent sur les estimations non biaisées de
. Les différentes méthodes d'évaluation de la mesure d'importance qui existent se concentrent sur les estimations non biaisées de  et
et  . Nous allons voir plus en détail deux de ces méthodes, dont une a été utilisée dans ce travail.
. Nous allons voir plus en détail deux de ces méthodes, dont une a été utilisée dans ce travail.
La méthode de Sobol' (Sobol', 1993) est une méthode Monte Carlo basée sur la variance (pour une discussion plus détaillée, voir Chan et al., 2000b). L'idée de cette méthode est de décomposer la fonction 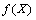 en sommes de dimensionnalité croissante:
en sommes de dimensionnalité croissante:
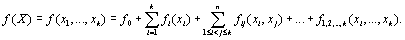 |
(6.16) |
Chaque terme de cette décomposition peut alors être traité par intégration Monte Carlo pour aboutir aux mesures de sensibilité 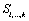 (une par terme de l'équation(6.16)) données par
(une par terme de l'équation(6.16)) données par
 |
(6.17) |
où  et
et 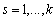 .
. 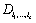 représente la variance partielle de chaque terme de l'équation (6.16) et
représente la variance partielle de chaque terme de l'équation (6.16) et  la variance totale de
la variance totale de  .
. 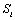 est appelé l'indice de sensibilité de premier ordre (first-order sensitivity analysis) du paramètre
est appelé l'indice de sensibilité de premier ordre (first-order sensitivity analysis) du paramètre  , et il mesure l'effet principal de
, et il mesure l'effet principal de 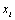 sur la réponse du modèle (la fraction de contribution de
sur la réponse du modèle (la fraction de contribution de 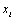 à la variance de
à la variance de  ).
).  (
( ) est quant à lui appelé indice de sensibilité de deuxième ordre (second-order sensitivity analysis), et il mesure l'effet d'interaction, autrement dit la partie de la variation de
) est quant à lui appelé indice de sensibilité de deuxième ordre (second-order sensitivity analysis), et il mesure l'effet d'interaction, autrement dit la partie de la variation de  due à
due à  et à
et à  qui ne peut pas être expliquée par la somme des effets individuels de
qui ne peut pas être expliquée par la somme des effets individuels de  et
et 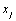 . Les indices de sensibilité d'ordre supérieur sont représentés de manière similaire. Une propriété importante des indices de sensibilité
. Les indices de sensibilité d'ordre supérieur sont représentés de manière similaire. Une propriété importante des indices de sensibilité  est que leur somme est égale à un. Notons que les variances partielles et la variance totale sont obtenues par intégration sur tout l'espace des paramètres, et selon un schéma semblable à celui employé lors d'une décomposition typique d'analyse de variance (ANOVA).
est que leur somme est égale à un. Notons que les variances partielles et la variance totale sont obtenues par intégration sur tout l'espace des paramètres, et selon un schéma semblable à celui employé lors d'une décomposition typique d'analyse de variance (ANOVA).
L'indice de sensibilité total (total sensitivity index, TSI) d'un paramètre est défini comme la somme de tous les indices de sensibilité qui prennent en compte le paramètre en question. Par exemple, pour un modèle à trois paramètres, l'effet total du paramètre 1 sur la réponse de modèle, noté  , est donné par
, est donné par 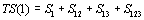 , où les différents termes de la partie droite de l'équation sont les indices de sensibilité d'ordre variable, comme expliqué au paragraphe précédent. L'indice de sensibilité total
, où les différents termes de la partie droite de l'équation sont les indices de sensibilité d'ordre variable, comme expliqué au paragraphe précédent. L'indice de sensibilité total 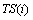 d'un paramètre
d'un paramètre  peut être noté
peut être noté
 |
(6.18) |
où  est la somme de tous les termes
est la somme de tous les termes  qui n'incluent pas l'index
qui n'incluent pas l'index  , c'est-à-dire la fraction de variation complémentaire au paramètre
, c'est-à-dire la fraction de variation complémentaire au paramètre 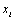 , notée
, notée  . La contribution totale du paramètre
. La contribution totale du paramètre 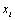 à la variation totale de la sortie du modèle est donnée par
à la variation totale de la sortie du modèle est donnée par
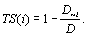 |
(6.19) |
Une des limitations des indices de sensibilité de Sobol' est leur coût de calcul. Lorsque le modèle étudié est non linéaire, le calcul des indices de sensibilité d'ordre supérieur est essentiel. Malheureusement, un échantillon séparé de taille N est nécessaire pour calculer chaque 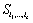 . Sachant que le nombre de termes de l'équation (6.16) est
. Sachant que le nombre de termes de l'équation (6.16) est  , il faut alors
, il faut alors 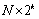 évaluations du modèle dans la méthode standard. Si le nombre de paramètres est grand, ce coût devient vite trop élevé. Des solutions ont néanmoins été trouvées pour réduire ce coût à
évaluations du modèle dans la méthode standard. Si le nombre de paramètres est grand, ce coût devient vite trop élevé. Des solutions ont néanmoins été trouvées pour réduire ce coût à  (Homma et Saltelli, 1996).
(Homma et Saltelli, 1996).
La méthode FAST (Fourier Amplitude Sensitivity Test), mise au point initialement par Cukier et al. (1973), et résumée dans Chan et al. (2000b) et dans Rahni (1998), permet d'estimer l'espérance et la variance de la réponse du modèle, ainsi que la contribution des paramètres individuels à cette variance, grâce aux propriétés des séries de Fourier. Cette méthode adresse donc en même temps l'analyse d'incertitude et l'analyse de sensibilité. L'idée principale de la méthode FAST est de convertir une intégrale à 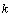 dimensions dans
dimensions dans  en une intégrale à une dimension dans
en une intégrale à une dimension dans  , en utilisant une fonction de transformation
, en utilisant une fonction de transformation 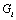 pour
pour  , soit
, soit
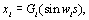 |
(6.20) |
où  est une variable scalaire et
est une variable scalaire et 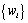 est un ensemble de fréquences angulaires entières. Autrement dit, une courbe de recherche (search curve) est utilisée pour scanner l'espace des paramètres, ce qui permet d'éviter l'intégration multidimensionnelle. L'application de la méthode FAST consiste alors à choisir
est un ensemble de fréquences angulaires entières. Autrement dit, une courbe de recherche (search curve) est utilisée pour scanner l'espace des paramètres, ce qui permet d'éviter l'intégration multidimensionnelle. L'application de la méthode FAST consiste alors à choisir  et
et  de manière appropriée et à évaluer le modèle un nombre de fois suffisant pour permettre l'évaluation numérique des intégrales qui définissent les coefficients de Fourier. Les indices de sensibilité de premier ordre sont calculés depuis les termes de la décomposition de Fourier. Les méthodes de calcul des indices de sensibilité totaux utilisant la méthode FAST ont été développées récemment dans ce qui est appelé la méthode FAST étendue (extended FAST (Saltelli et al., 1999)). Ces calculs sont effectués par analogie avec ce qui a été décrit pour les indices totaux dans la méthode de Sobol' (équation (6.19)).
de manière appropriée et à évaluer le modèle un nombre de fois suffisant pour permettre l'évaluation numérique des intégrales qui définissent les coefficients de Fourier. Les indices de sensibilité de premier ordre sont calculés depuis les termes de la décomposition de Fourier. Les méthodes de calcul des indices de sensibilité totaux utilisant la méthode FAST ont été développées récemment dans ce qui est appelé la méthode FAST étendue (extended FAST (Saltelli et al., 1999)). Ces calculs sont effectués par analogie avec ce qui a été décrit pour les indices totaux dans la méthode de Sobol' (équation (6.19)).
Un avantage de la méthode FAST est que l'évaluation des indices de sensibilité peut être menée indépendamment pour chaque paramètre en utilisant un seul ensemble d'évaluation du modèle. Les indices de sensibilité totaux sont donc calculés en même temps que les indices de premier ordre, et ne demandent pas un ensemble supplémentaire d'évaluation du modèle, comme c'est le cas avec la méthode de Sobol'. Le nombre d'évaluations du modèle avec la méthode FAST est de 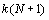 , donc deux fois moins élevé qu'avec la méthode de Sobol'. Un
, donc deux fois moins élevé qu'avec la méthode de Sobol'. Un 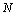 de 200 est généralement conseillé (Stefano Tarantola, comm. pers.). Néanmoins, un désavantage de la méthode FAST, par rapport à celle de Sobol', est qu'elle peut être biaisée lorsque la distribution des paramètres d'entrée est uniforme discrète (Stefano Tarantola, comm. pers.). Une amélioration de la méthode pour pallier à cet inconvénient est néanmoins en cours et devrait être bientôt disponible.
de 200 est généralement conseillé (Stefano Tarantola, comm. pers.). Néanmoins, un désavantage de la méthode FAST, par rapport à celle de Sobol', est qu'elle peut être biaisée lorsque la distribution des paramètres d'entrée est uniforme discrète (Stefano Tarantola, comm. pers.). Une amélioration de la méthode pour pallier à cet inconvénient est néanmoins en cours et devrait être bientôt disponible.
Les méthodes basées sur la variance, décrites dans ce chapitre, sont dites quantitatives car elles permettent de calculer des indices de sensibilité, pour chacun des paramètres, qui sont sommés à un. D'autres techniques ne peuvent capturer que les effets additifs (de premier ordre) et peuvent être considérées comme quantitatives seulement si le modèle est additif. Les méthodes Sobol' et FAST étendue ont été développées afin de minimiser le nombre d'évaluations du modèle, tout en permettant un calcul robuste des indices de premier ordre et totaux. Le nombre d'évaluations d'un modèle peut néanmoins être trop élevé pour des modèles où le temps d'exécution d'une simulation est grand. Une façon de remédier en partie à ce problème est de générer des sous-groupes de paramètres qui sont traités comme une seule entité. Ceci est particulièrement motivé lorsque un modèle est constitué de plusieurs sous-modèles ou modules (comme c'est le cas de FRICTION). La conséquence de ce groupement est que le nombre d'évaluations du modèle est réduit, et qu'une représentation plus compacte des résultats est possible. Le désavantage étant que l'on perd alors les mesures d'importance des paramètres individuels au sein d'un sous-groupe.
6.7.3. Résultats tabulaires
Les résultats ci-dessous regroupent les données tabulaires des analyses de sensibilité utilisant la méthode FAST. Les descriptions des facteurs, des réponses étudiées et des résultats se trouvent aux chapitres 0 et 4.6.4. Les valeurs de capacité de soutien et de friction utilisées (dans les modèles où ces valeurs ne varient pas) se trouvent à la fin de cette Annexe.
6.8. Coordonnées des origines et échantillons
Nous donnons ici les coordonnées des origines (Tableau 6.13.) et des échantillons (Tableau 6.14.) utilisés pour les méthodes d'assignation. Les représentations visuelles de ces points ont été données dans la Figure 4.39.
Les latitudes (Lat) et les longitudes (Long) sont données en degrés décimaux (dd) et en kilomètres (km) lorsque les données sont utilisées en projection de Hammer. Le choix des localisations s'est fait sur la base d'une partie des échantillons du HGDP (Human Genome Diversity Project) et du CEPH (Centre d'Étude du Polymorphisme Humain) (voir Cann et al., 2002). Pour compléter la répartition géographique de ces échantillons, nous avons ajouté cinq localisations qui sont marquée par un astérisque.
6.9. Programmes CORRELATOR et REGIONS
6.9.1 CORRELATOR
Le programme CORRELATOR a été utilisé pour les différents tests d'assignation d'origine du chapitre 0 Les étapes de calculs effectuées par ce programme ont été décrites dans le chapitre 0 Ce programme est écrit en C++ et s'utilise uniquement en ligne de commande. Il a été utilisé essentiellement sous Linux, mais il peut tout aussi bien être compilé sous l'environnement Windows.
Ce programme peut prendre de zéro à trois paramètres, suivant la synopsis suivante:
CORRELATOR [fichier d'entrée] [n° de l'origine considérée] ([nombre de locus])
fichier d'entrée: nom (avec extension) du fichier texte contenant les matrices de FST linéarisées. Ce fichier est le fichier de sortie du script make_multilocus_files.sh
n° de l'origine considérée: ce nombre indique le numéro de l'origine considérée comme origine focale dans les calculs d'assignation. Comme le programme CORRELATOR est typiquement utilisé sur le cluster Linux, chaque noeud du cluster va travailler sur une origine.
nombre de locus: si ce troisième paramètre existe, il indique combien de locus doivent être considérés pour générer un nouveau fichier d'entrée multilocus. Le programme CORRELATOR est alors utilisé comme générateur de fichiers multilocus.
Avec les deux premiers paramètres, les fichiers de sorties du programme CORRELATOR sont au nombre de trois, et sont tous sous une forme matricielle:
assignmentValues*.out: contient les scores d'assignation à chaque origine pour les sept percentiles de la distribution des corrélations
meanValues*.out: contient les valeurs moyennes de corrélation à chaque origine pour les sept percentiles de la distribution des corrélations
summaryTable*.out: contient les fréquences moyennes d'assignation à l'origine focale pour les sept percentiles de la distribution des corrélations
Où * est à remplacer par le numéro de l'origine focale considérée.
6.9.2. REGIONS
Le programme REGIONS a été développé pour les besoins des tests d'assignation régionale du chapitre 0 Ce programme permet de définir un nombre arbitraire de régions composées chacune d'un certain nombre d'origine. Chaque région se comporte comme une entité géographique, et les calculs d'assignation se font alors par région, plutôt que par origine comme dans le programme CORRELATOR. Ce programme est écrit en C++ et s'utilise uniquement en ligne de commande. Il a été utilisé essentiellement sous l'environnement Windows, mais il peut tout aussi bien être compilé sous Linux.
Ce programme peut prendre de zéro à deux paramètres, suivant la synopsis suivante:
REGIONS [fichier de paramètre] ([nombre de simulation])
fichier de paramètre: nom (avec extension) du fichier texte définissant les régions. La première ligne du fichier contient le nombre d'origines suivis du nombre de région. Chaque ligne suivante définit une région, en indiquant premièrement le nombre d'origines constituant la région (en gras ci-dessous), suivi des identificateurs de chaque origine de la région. Chaque identificateur d'origine ne doit apparieur que dans une seule région.

nombre de simulation: ce deuxième paramètre permet d'indiquer combien de simulation ont été utilisées pour aboutir aux fichiers d'assignation. La valeur par défaut est 5'000.
Le programme REGIONS travaille avec l'ensemble des fichiers de résultats assignmentValues*.out (où * est à remplacer par le numéro de l'origine focale considérée) obtenus par le programme CORRELATOR. REGIONS doit être utilisé dans le même dossier où se trouvent ces fichiers de résultats. Le fichier de sortie 'Regions_results.txt' est sous une forme matricielle:
| Région | Score | Fréquence |
| 1 | 12894/17500(7) | 0.737 |
| 2 | 19436/25000(10) | 0.777 |
| 3 | 12854/15000(6) | 0.857 |
| 4 | 685/5000(2) | 0.137 |
| Total | 45869/62500 | 0.734 |
Les scores sont donnés pour chaque région selon: nombre d'assignations dans la région/nombre total de simulations depuis cette région (nombre d'origines dans la région). Les fréquences de bonne assignation sont ensuite données.
6.10. Méthodes d'échantillonnage multilocus
Dans le contexte des tests d'assignation d'origine qui ont été abordés au chapitre 4.7., cette Annexe discute de deux méthodes d'échantillonnages multilocus et de l'impact de leurs utilisations sur les résultats.
Dans les discussions qui suivent, une matrice de 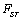 par paire (linéarisée en une ligne dans le fichier de résultats) est appelée une simulation. Lorsqu'un fichier de simulation est rééchantillonné pour aboutir à un fichier multilocus, chaque ligne de ce nouveau fichier est alors appelée une simulation multilocus.
par paire (linéarisée en une ligne dans le fichier de résultats) est appelée une simulation. Lorsqu'un fichier de simulation est rééchantillonné pour aboutir à un fichier multilocus, chaque ligne de ce nouveau fichier est alors appelée une simulation multilocus.
Pour obtenir un fichier de résultat multilocus sur n locus, nous pouvons combiner les résultats de n simulations de coalescence, puisque l'histoire généalogique de chaque locus est par définition indépendante. Cette combinaison des résultats des simulations peut se faire selon deux méthodes. La première consiste à considérer des groupes de n simulations indépendantes, et de calculer un indice 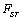 moyen par groupe. Cette technique aboutit à un nombre de simulations multilocus de N/n, si N est le nombre total de simulation. Avec 5000 simulations génétiques, nous aurons donc 50 simulations multilocus, si 100 locus sont considérés conjointement. L'avantage de cette méthode est donc de travailler avec des groupes de simulations complètement indépendants, mais elle a le désavantage d'aboutir à un nombre réduit de simulations multilocus et augmente de ce fait la variance des résultats.
moyen par groupe. Cette technique aboutit à un nombre de simulations multilocus de N/n, si N est le nombre total de simulation. Avec 5000 simulations génétiques, nous aurons donc 50 simulations multilocus, si 100 locus sont considérés conjointement. L'avantage de cette méthode est donc de travailler avec des groupes de simulations complètement indépendants, mais elle a le désavantage d'aboutir à un nombre réduit de simulations multilocus et augmente de ce fait la variance des résultats.
La deuxième méthode d'obtention des résultats multilocus consiste à échantillonner, N fois et avec remise, des groupes de n simulations parmi les N simulations disponibles. Cette méthode a l'avantage d'aboutir à N résultats multilocus, mais peut potentiellement introduire un biais dû à des résultats de simulations qui seraient partagés par plusieurs groupes de simulations.
Pour tester l'influence de ces deux méthodes sur les résultats d'assignation d'origine, nous avons comparé un jeu de simulations multilocus obtenus avec la première méthode (échantillonnage par bloc) avec jeu de simulations multilocus obtenus avec la seconde méthode (échantillonnage aléatoire). Les résultats des fréquences moyennes d'assignation se trouvent dans la Figure 6.14, alors que les résultats spécifiques au percentile 90% et leurs écart-types associés sont montrés dans la Figure 6.15.
Au vu de ces deux figures, nous remarquons un biais systématique de l'échantillonnage aléatoire qui a tendance à augmenter les fréquences d'assignation par rapport à l'échantillonnage par bloc. Cela démontre qu'il subsiste une composante d'autocorrélation lorsque des simulations sont échantillonnées aléatoirement. Cela est dû au fait que nous générons autant de simulations multilocus qu'il n'y a de simulations initiales: il y a donc forcément certaines simulations multilocus qui partagent une, voir plusieurs, simulations initiales identiques. Comme attendu, la variance des résultats pour l'échantillonnage par bloc est plus grande (voir les écart-types de la Figure 6.15, car les distributions de corrélation sous cette méthode comportent moins de points.


Les écart-types de chaque valeur sont également indiqués et sont reliés par des pointillés.
Nous remarquons cependant que, pour le percentile 90%, le proportion du biais introduit est la même qu'elle que soit le nombre de locus. Dans les applications du chapitre 4.7.4, les différentes configurations environnementales ont été différenciées en analysant les différences de valeurs aux percentiles 90%. Une plus grande variance sur ces percentiles aurait souvent rendu plus difficiles ces comparaisons. Nous avons donc choisi de travailler avec la méthode d'échantillonnage aléatoire, qui permet d'obtenir des distributions d'un plus grand nombre de corrélations (5000).
6.11. Résultats des études d'assignation
Cette Annexe présente certains résultats tabulaires des études sur les assignations d'origine présentés au chapitre 4.7.4.
Ces valeurs ont été discutées dans le chapitre 4.7.4.5. Les scores sont donnés selon: nombre d'assignations selon un type de scénario/nombre total de simulation avec ce type de scénario (nombre de scénario).
 est la proportion.
est la proportion.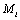 , et de la densité locale
, et de la densité locale 




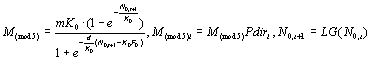
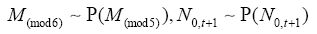

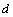
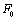
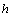
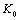

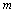
 .
.