RealPSPA

Description

RealPSPA implements in MATLAB, the criss-cross algorithm for computing the real \(\varepsilon\)–pseudospectral abscissa of a real matrix \(A\in {\mathbb R}^{n\times n}\):

\[ \alpha_\varepsilon^{\mathbb R}(A) =\max \left\{\mbox{Re}(\lambda)\, \colon\, \lambda \in \Lambda_{\varepsilon}^\mathbb R(A)\right\}, \]

where

\[ \Lambda_{\varepsilon}^ \mathbb R (A) = \left\{\lambda \in \mathbb C: \lambda \in \Lambda(A+E) \mbox{ with }E\in \mathbb R^{n\times n}, \|E\|_2\leq \varepsilon \right\}, \]

and \(\Lambda(A)\) denotes the eigenvalues of a matrix.

This package contains functions suitable for both dense and large sparse matrices \(A\). A detailed description of the algorithms can be found in the paper Ref. [1].

Authors

• Ding Lu (University of Geneva)

• Bart Vandereycken (University of Geneva)

Contents

Main files

• Main functions:

  • rpsa.m: Criss-cross algorithm, suitable for small to medium size matrix \(A\) (say \(n\leq 1\mbox{k}\)).

  • rpsas.m: Criss–cross combined with subspace methods, suitable for large sparse \(A\).

• Package download link RealPSPA_v01.tar.gz — (updated on June 13th, 2016).

• Remarks: The code should work for any (relatively recent) version of MATLAB. It was tested on 2013b, 2016a (LINUX). We encourage users to run the code with 2016a, due to its new features in the svds function called by rpsas.

Auxiliary files

Data and demo routines for numerical examples in Ref. [1].

• Download link rpsa_examples.tar.gz — (updated on June 13th, 2016).

• Remarks: For a few examples, we need EigTool for data matrices generating, and the low–rank dynamical algorithm (Rostami's) for performance comparison. Please download these packages using the links below.

  • EigTool: http://www.comlab.ox.ac.uk/pseudospectra/eigtool/

  • Rostami's Algorithm: http://users.wpi.edu/~mwu/webpage_code/pseudo/

Use of the code

Permission to use, copy,and modify this software for any purpose and without fee is hereby granted. For publications that uses this software, a reference to the paper, Ref. [1] below, will be appreciated.

Examples

See Ref. [1] for details.

I. Criss-cross methods: rpsa

Fig. I.a: Demmel 3–by–3 matrix, \(\varepsilon=10^{-3.2}\). Black line: boundary of \(\Lambda_{\varepsilon}^{\mathbb R}(A)\); Colored line: boundary of supersets used in each criss-cross iteration; Mark \(\mathtt o\): approximate rightmost point.

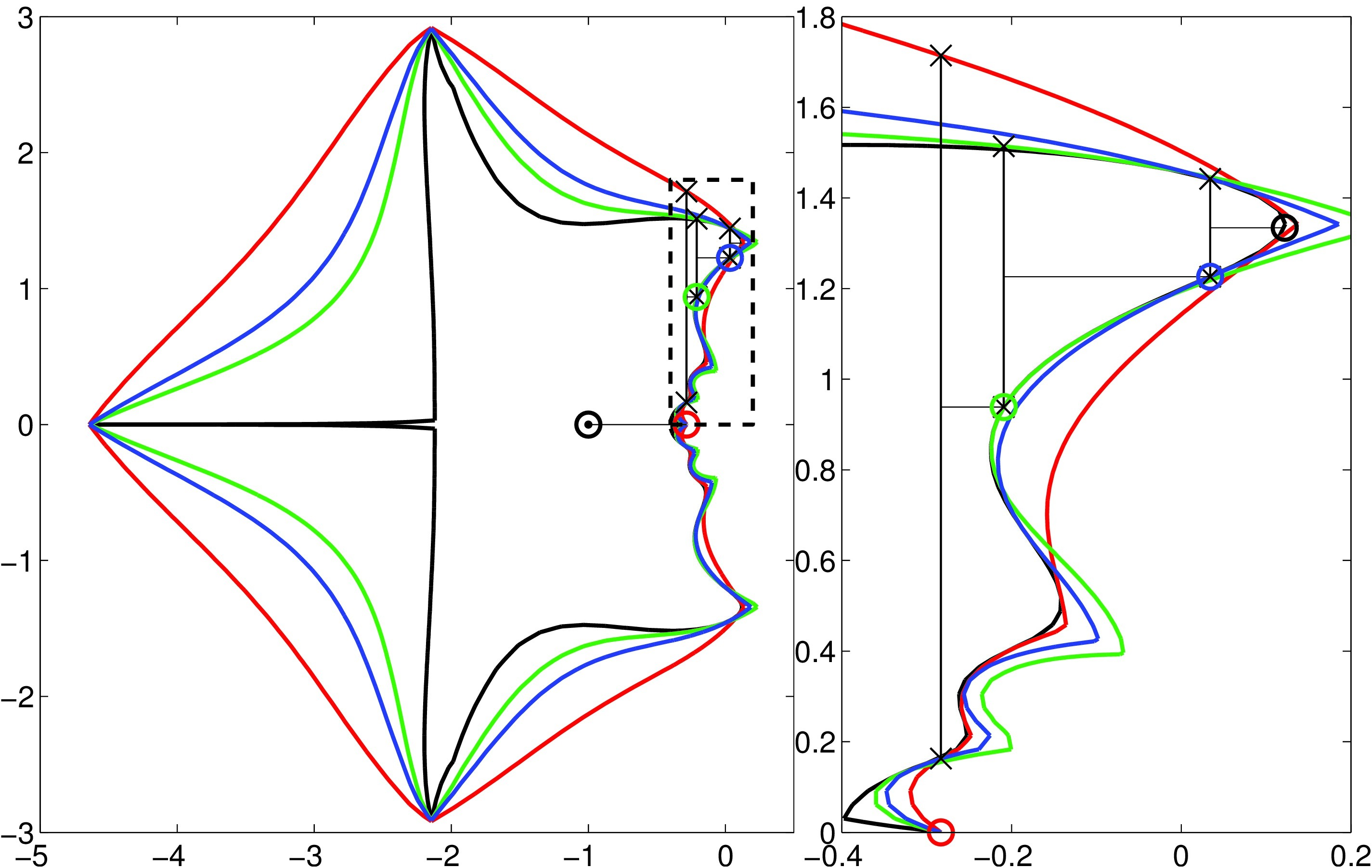Fig. I.b: Demmel 5–by–5 matrix, \(\varepsilon=10^{-2}\). First 3 iterations, same figure setting as above.

II. Criss-cross + subspace methods: rpsas — (eig mode)

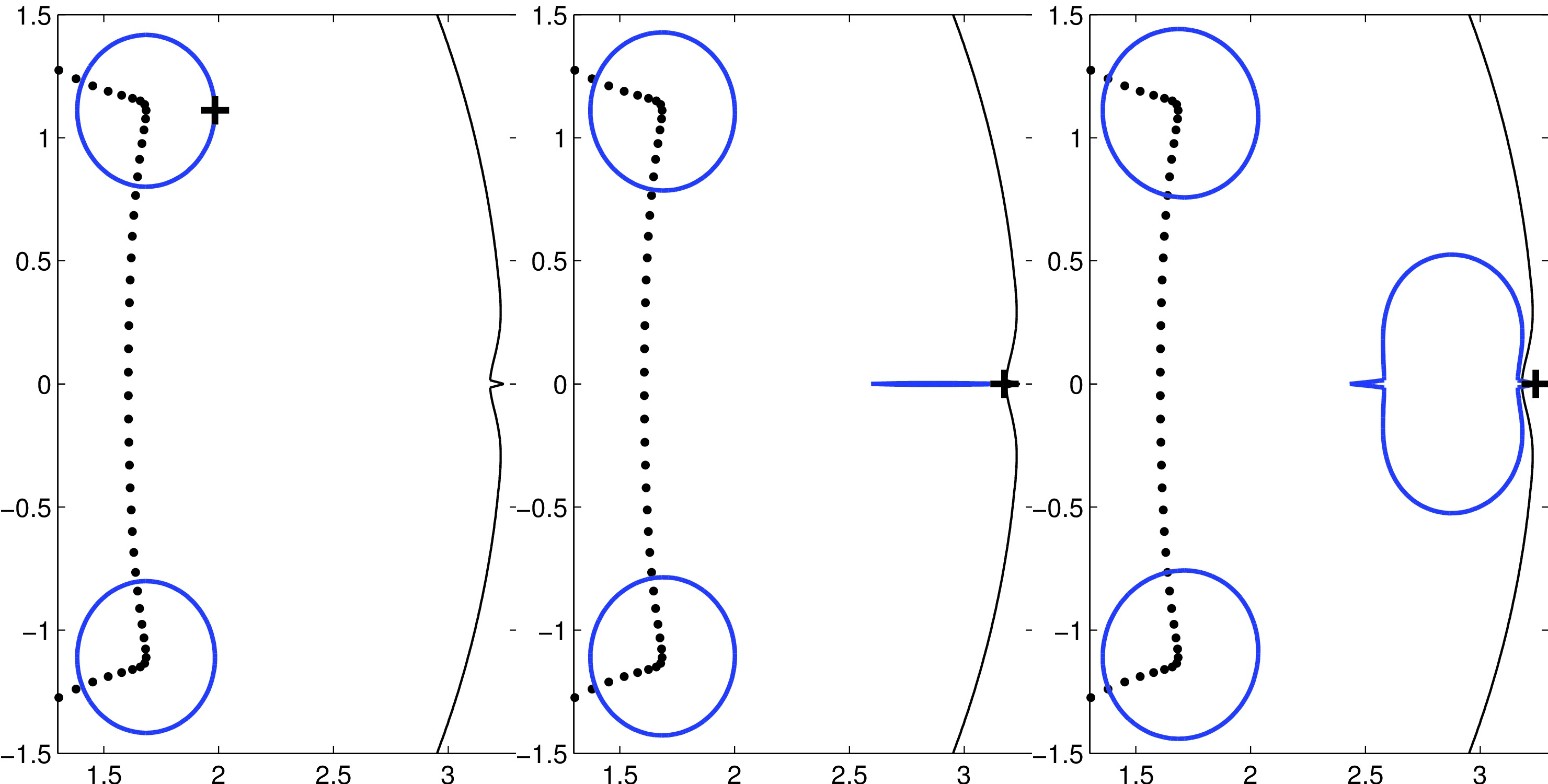Fig. II.a: Grcar(100) matrix, \(\varepsilon=0.3\), iterations k= 1, 2, 4. Black line: boundary of \(\Lambda_\varepsilon^\mathbb R(A)\); Blue line: boundary of the reduced \(\Lambda_\varepsilon^\mathbb R(AV_k,V_k)\); Mark +: approximate rightmost point in kth itration.

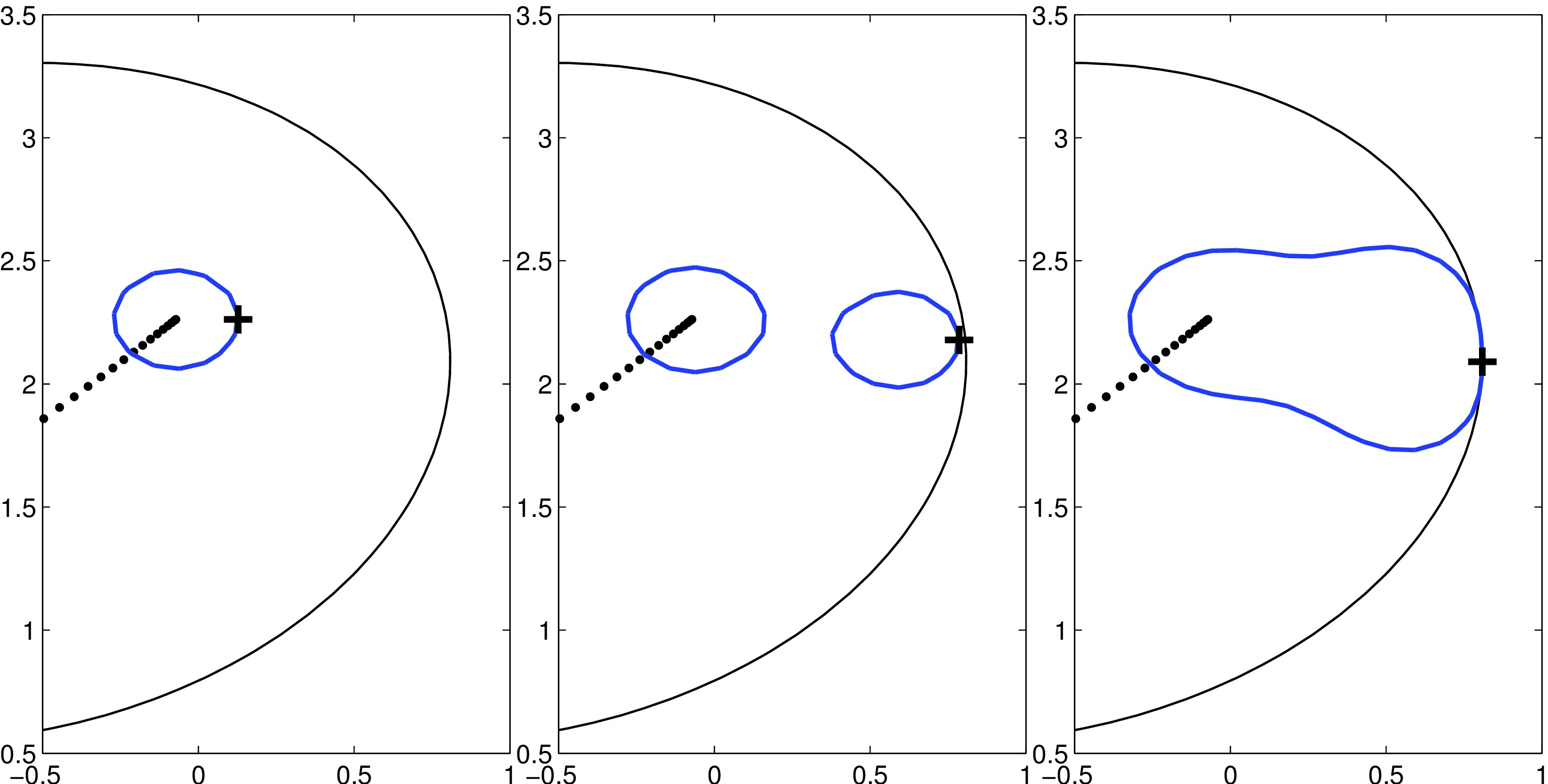Fig. II.b: \(-\)Grcar(100) matrix, \(\varepsilon=0.2\), iterations k= 1, 2, 5. Same figure setting as above.

References

1. Criss-cross type algorithms for computing the real pseudospectral abscissa
   by Ding Lu and Bart Vandereycken
   SIAM J. Matrix Anal. Appl., 2017. 38(3):891–923. (paper)

Release notes

• Released June 13, 2016

Contact

Email: Ding.Lu@unige.ch
Homepage: http://www.unige.ch/~dlu