Following on from the interactive book Mathema and using the experience gained from many Mathema-based workshops, Hugo Parlier and I teamed up with Mario Gutiérrez (who was the main developer for Mathema) and Reyna Juárez to create new platforms for interactive mathematical puzzles under the name Quadratis.

The aim is educational - we believe that the kind of mathematical games and puzzles we are making can both inspire children and adults alike, dispel the common belief that math is only "equations" and simply provide fertile ground for encouraging modes of thinking found in mathematics and science. Also, the puzzles are rather addictive and just a bit of simple entertainment!

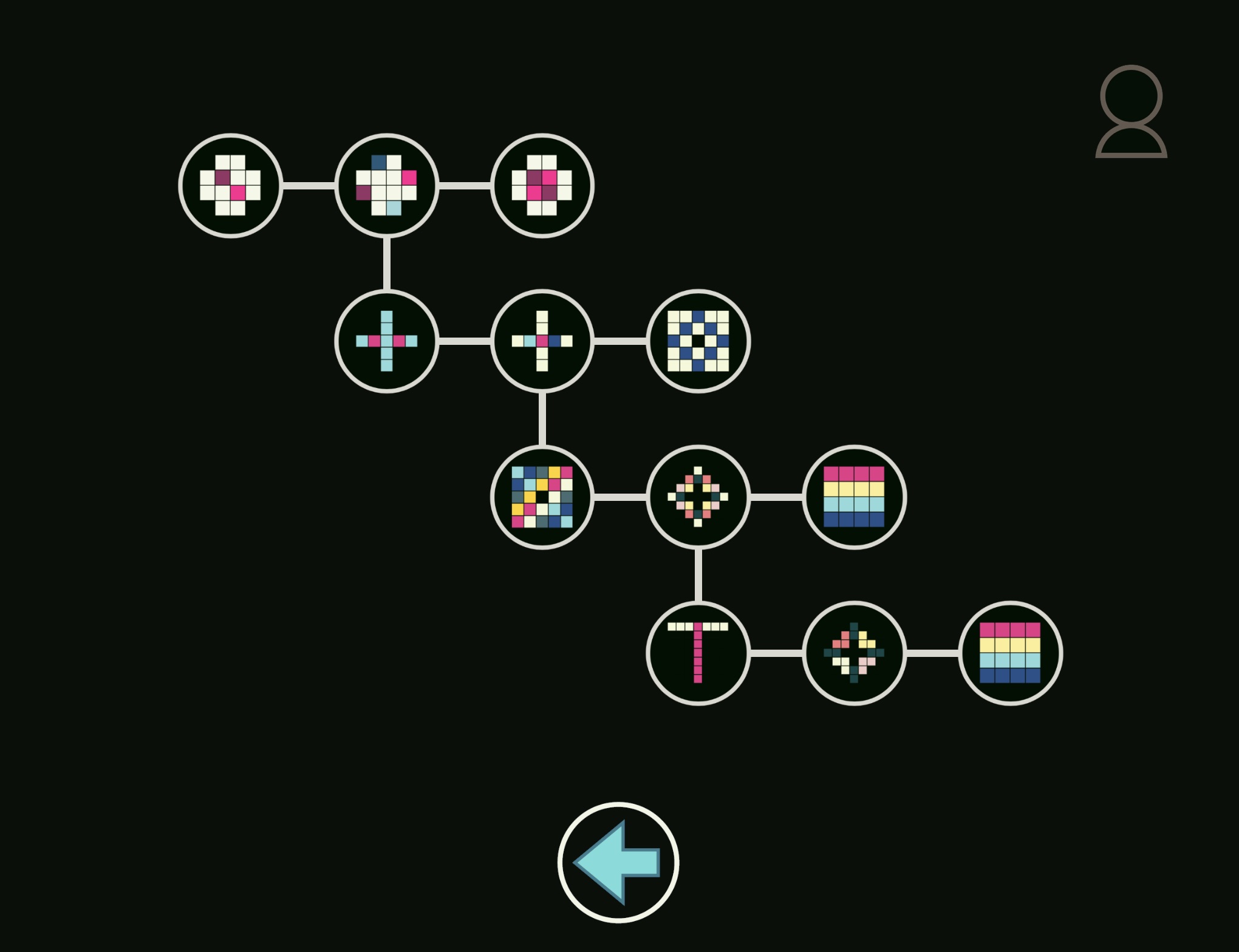
So far the main outputs are science museum exhibit, called Exploratis , developed in conjunction with (and now installed in) the Luxembourg Science Centre, and Quadratis - Game consisting of 16 puzzles packaged into an app. Both of these are based on extending the "chromasquares" that we wrote about in Mathema.

Exploratis

In addition to its permanent home in the Luxembourg Science Center, Exploratis was chosen to showcase at the Luxembourg pavillion at World Expo 2020 in Dubai. It was featured there from December 12th to 16th, 2021. Some photos from Dubai can be found here.

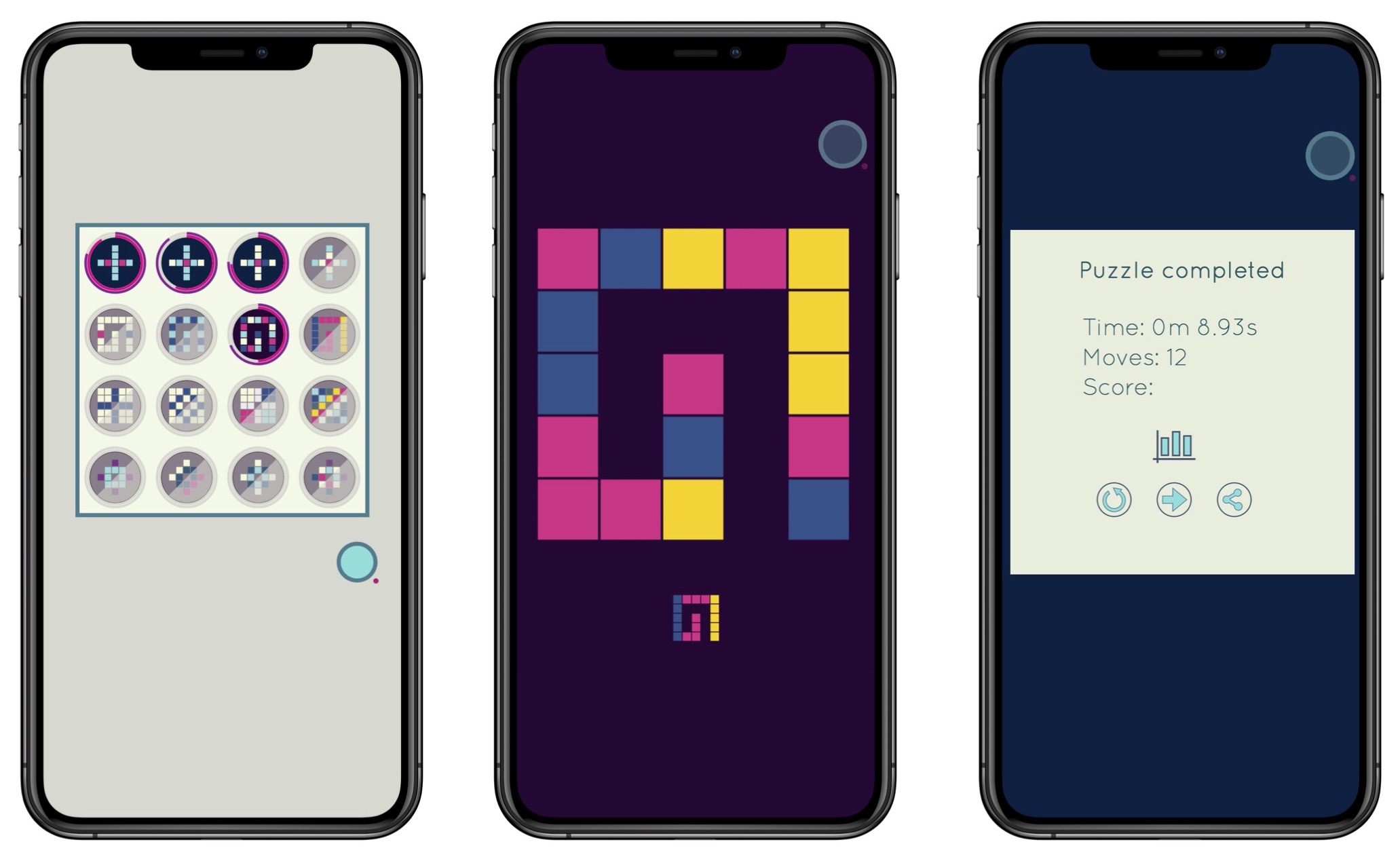
The installation consists of two iPads arranged face-to-face on custom-made stands adjacent to a large screen. The players may play individually or they may compete in a race or they may decide to work together in collaborative mode.

Each player's screen displays a puzzle to be solved: the aim is to scroll columns and rows to reproduce a pre-defined "home" configuration. The big screen displays a portion of the "configuration graph" which unfolds as the players unravel the puzzle.

Quadratis - Game

In its initial version this consists of 16 puzzles, along with a brief tutorial presented in the form of an app. Points are scored based on time taken and number of moves needed to solve a particular puzzle. Basic stats recording performace are included.

A preliminary version is already available on the App Store (free download).

Where is the math ?

Each Quadratis puzzle has hundreds, or thousands or millions or many billions of attainable possible colour configurations. From left to right the puzzles shown below have respectively 630 configurations, around 18 thousand, around 1.2 million and around 3 million billion configurations.

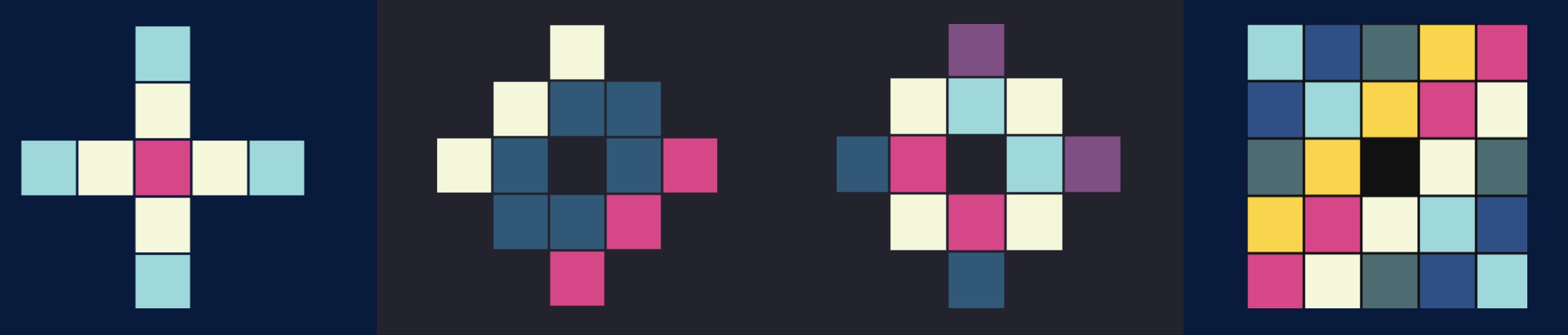
Configurations may be transformed by row or column moves: swipe a row left-to-right and all the squares on that row are moved along by one place. The square which drops off the end is re-attached in the easiest cases in a cyclical way. In fact more complicated "side identifications" may be made (resulting in harder puzzles) and by gluing up the identified edges one gets a so-called square tiled surface. These play an important role in moduli space theory.

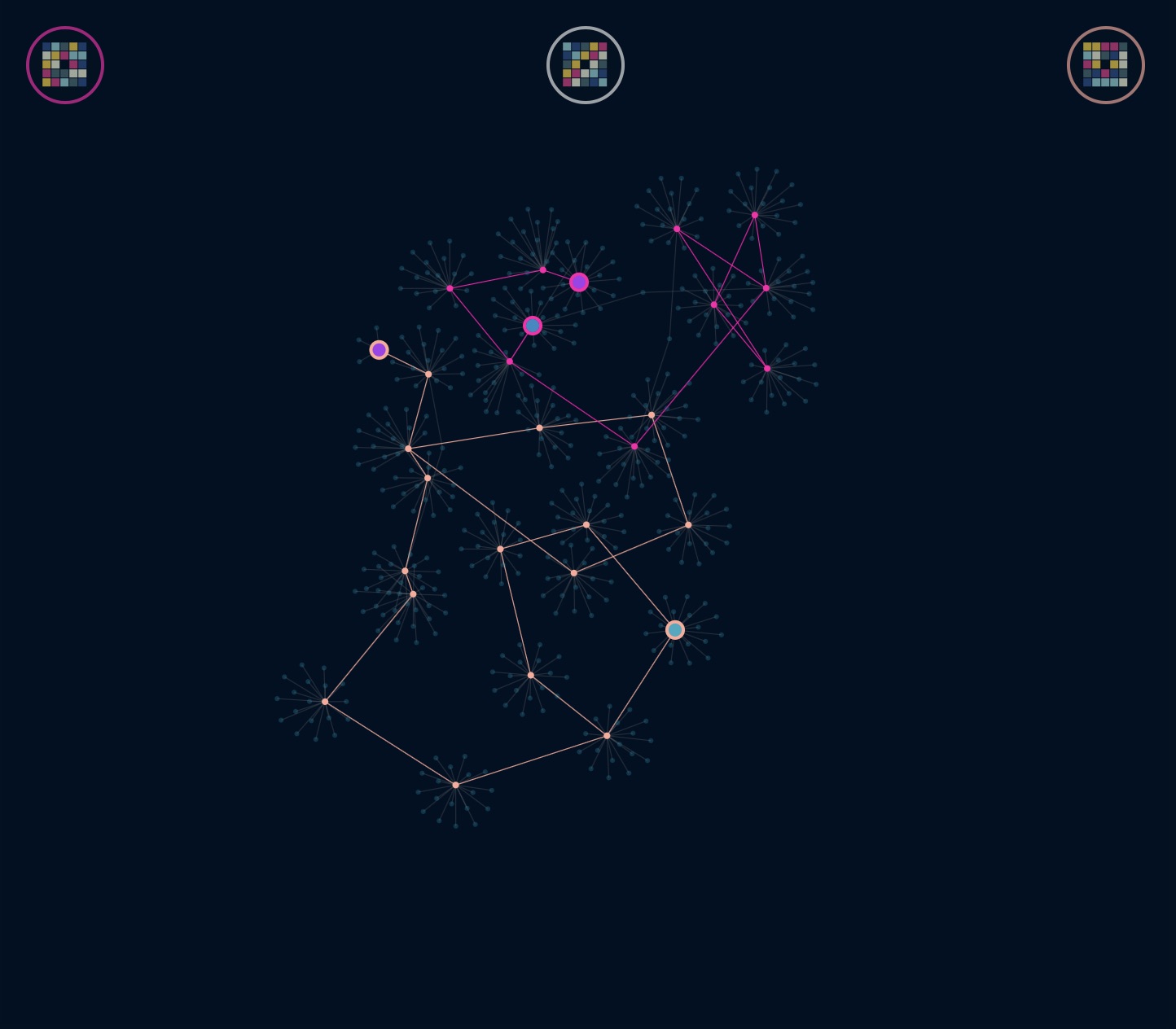
Intuitively two different configurations are “close” if we can transform one to the other by few horizontal or vertical moves. The immediate neighbours of a given configuration are those that can be obtained by a single row or column swipe move. We can make a graph (or network) in the following way: each possible configuration is a vertex (or node) and we join two vertices by an edge if they differ by a single move. It is this entire network which provides us with an interesting mathematical object.

Here is the entire network of the left-most puzzle shown above.