Geneva's Chalk Talks - Jehanne Dousse

The blackboard displays several aspects of the theory of partition identities, a topic that arose in combinatorics but has strong and interesting connections with other topics such as number theory, representation theory, commutative algebra or mathematical physics.
A partition of a positive integer n is a non-increasing sequence of positive integers whose sum is n, the partitions of 3 being (3), (2,1) and (1,1,1). A partition identity is a theorem asserting that for all n, the number of partitions of n satisfying some conditions equals the number of partitions of n satisfying some other conditions.

The first blackboard displays one of the most important partition identities in the literature: the Andrews-Gordon identities. They can be written either in analytic form, as a q-series identity (infinite sum = infinite product), or in a combinatorial form. An important particular case is the Rogers-Ramanujan identities, stating that for all n, there are as many partitions of n such that consecutive parts differ by at least 2 as partitions of n into parts congruent to 1 or 4 modulo 5. These identities arise naturally in several fields of mathematics, as we will see in the next boards.
The second board (see the full board at the end for a better view) displays the fascinating connection between partition identities and the representation theory of affine Lie algebras. After performing some specialisations, the character of certain Lie algebra representations can be seen as an infinite product, or equivalently as the generating function for partitions with congruence conditions. For example, the product side of the Rogers-Ramanujan identities is related to the characters of level 3 standard modules of the Lie algebra A1(1). For the sum side, or equivalently partitions with difference conditions, using perfect crystals and the theory of grounded partitions that I developed with Isaac Konan, one can express the character as a generating function for coloured partitions satisfying difference conditions.
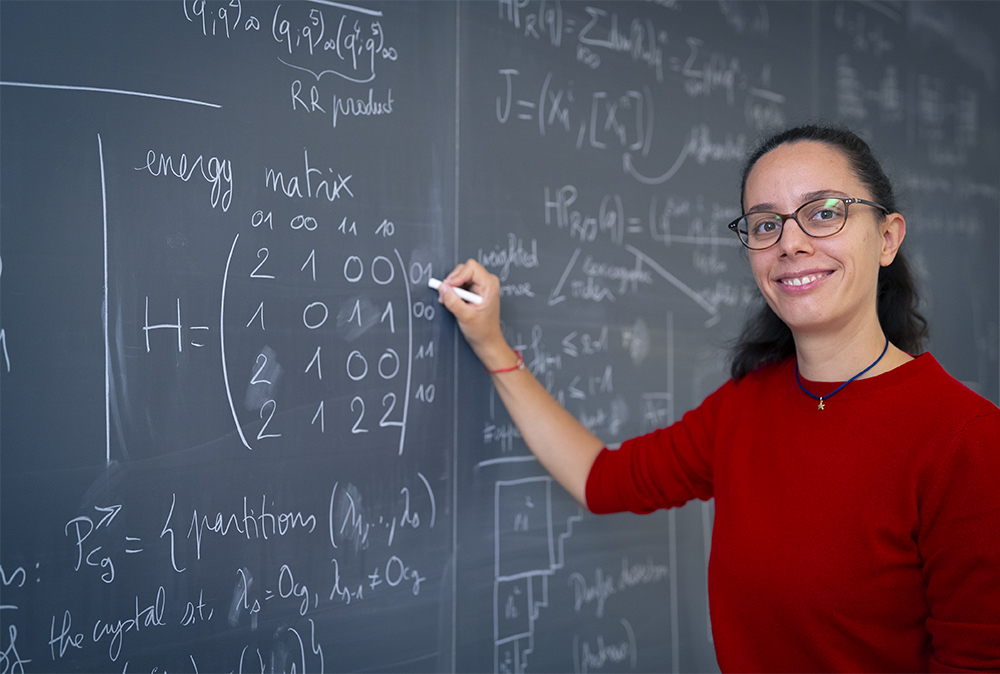

The third board illustrates the connection between the Andrews-Gordon identities and commutative algebra. It shows that the sum-side of these identities can be seen as the Hilbert-Poincaré series of a an algebra of polynomials quotiented by a certain differential ideal. Taking different orders on the monomials gives rise to different combinatorial interpretations, as can be seen on the drawing at the bottom of the board.
Finally, the fourth board shows a bijective process invented by Warnaar and which I recently generalised with my coauthors, which consists in writing partitions as particles and moving these particles according to specific rules. This allows to prove bijectively that the sum-side of the Andrews-Gordon identities is indeed the generating function for partitions such that the total number of occurrences of consecutive parts is at most k, and to prove many classical and new partition identities.


Jehanne Dousse obtained her PhD from Université Paris 7 in 2015. After a postdoctoral fellowship at Universität Zürich, she joined CNRS in 2018 as “chargée de recherche” at Université Claude Bernard Lyon 1. Since September 2022, she is an Eccellenza assistant professor at UNIGE. Her research interests lie at the intersection between combinatorics, number theory and representation theory.
Images: Manu Zirnheld (UNIGE)
